A survey of probabilistic generative frameworks for molecular simulations

Generative artificial intelligence is now a widely used tool in molecular science. Despite the popularity of probabilistic generative models, numerical experiments benchmarking their performance on molecular data are lacking. In this work, we introduce and explain several classes of generative models, broadly sorted into two categories: flow-based models and diffusion models. We select three representative models: Neural Spline Flows, Conditional Flow Matching, and Denoising Diffusion Probabilistic Models, and examine their accuracy, computational cost, and generation speed across datasets with tunable dimensionality, complexity, and modal asymmetry. Our findings are varied, with no one framework being the best for all purposes. In a nutshell, (i) Neural Spline Flows do best at capturing mode asymmetry present in low-dimensional data, (ii) Conditional Flow Matching outperforms other models for high-dimensional data with low complexity, and (iii) Denoising Diffusion Probabilistic Models appears the best for low-dimensional data with high complexity. Our datasets include a Gaussian mixture model and the dihedral torsion angle distribution of the Aib\textsubscript{9} peptide, generated via a molecular dynamics simulation. We hope our taxonomy of probabilistic generative frameworks and numerical results may guide model selection for a wide range of molecular tasks.

Graph Neural Network-State Predictive Information Bottleneck (GNN-SPIB) approach for learning molecular thermodynamics and kinetics

Molecular dynamics simulations offer detailed insights into atomic motions but face timescale limitations. Enhanced sampling methods have addressed these challenges but even with machine learning, they often rely on pre-selected expert-based features. In this work, we present the Graph Neural Network-State Predictive Information Bottleneck (GNN-SPIB) framework, which combines graph neural networks and the State Predictive Information Bottleneck to automatically learn low-dimensional representations directly from atomic coordinates. Tested on three benchmark systems, our approach predicts essential structural, thermodynamic and kinetic information for slow processes, demonstrating robustness across diverse systems. The method shows promise for complex systems, enabling effective enhanced sampling without requiring pre-defined reaction coordinates or input features.

Generative artificial intelligence for computational chemistry: a roadmap to predicting emergent phenomena

The recent surge in Generative Artificial Intelligence (AI) has introduced exciting possibilities for computational chemistry. Generative AI methods have made significant progress in sampling molecular structures across chemical species, developing force fields, and speeding up simulations. This Perspective offers a structured overview, beginning with the fundamental theoretical concepts in both Generative AI and computational chemistry. It then covers widely used Generative AI methods, including autoencoders, generative adversarial networks, reinforcement learning, flow models and language models, and highlights their selected applications in diverse areas including force field development, and protein/RNA structure prediction. A key focus is on the challenges these methods face before they become truly predictive, particularly in predicting emergent chemical phenomena. We believe that the ultimate goal of a simulation method or theory is to predict phenomena not seen before, and that Generative AI should be subject to these same standards before it is deemed useful for chemistry. We suggest that to overcome these challenges, future AI models need to integrate core chemical principles, especially from statistical mechanics.

Enhanced sampling of Crystal Nucleation with Graph Representation Learnt Variables

In this study, we present a graph neural network-based learning approach using an autoencoder setup to derive low-dimensional variables from features observed in experimental crystal structures. These variables are then biased in enhanced sampling to observe state-to-state transitions and reliable thermodynamic weights. Our approach uses simple convolution and pooling methods. To verify the effectiveness of our protocol, we examined the nucleation of various allotropes and polymorphs of iron and glycine from their molten states. Our graph latent variables when biased in well-tempered metadynamics consistently show transitions between states and achieve accurate free energy calculations in agreement with experiments, both of which are indicators of dependable sampling. This underscores the strength and promise of our graph neural net variables for improved sampling. The protocol shown here should be applicable for other systems and with other sampling methods.

Enhanced Sampling with Machine Learning: A Review

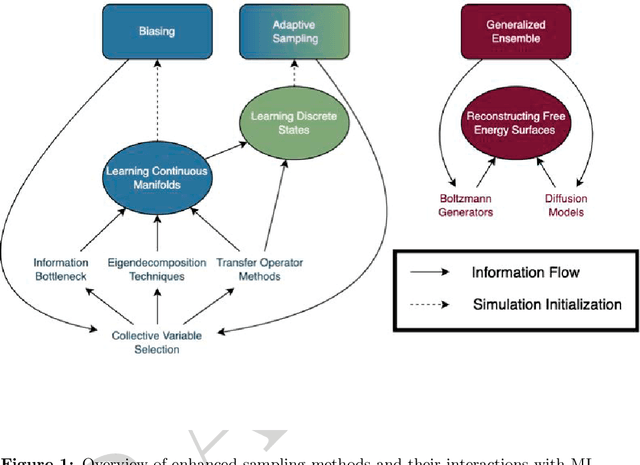
Molecular dynamics (MD) enables the study of physical systems with excellent spatiotemporal resolution but suffers from severe time-scale limitations. To address this, enhanced sampling methods have been developed to improve exploration of configurational space. However, implementing these is challenging and requires domain expertise. In recent years, integration of machine learning (ML) techniques in different domains has shown promise, prompting their adoption in enhanced sampling as well. Although ML is often employed in various fields primarily due to its data-driven nature, its integration with enhanced sampling is more natural with many common underlying synergies. This review explores the merging of ML and enhanced MD by presenting different shared viewpoints. It offers a comprehensive overview of this rapidly evolving field, which can be difficult to stay updated on. We highlight successful strategies like dimensionality reduction, reinforcement learning, and flow-based methods. Finally, we discuss open problems at the exciting ML-enhanced MD interface.

Introducing dynamical constraints into representation learning

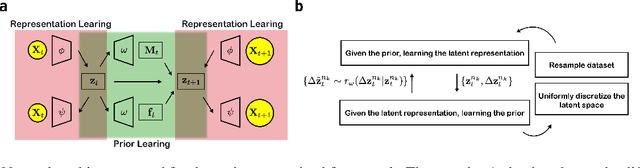
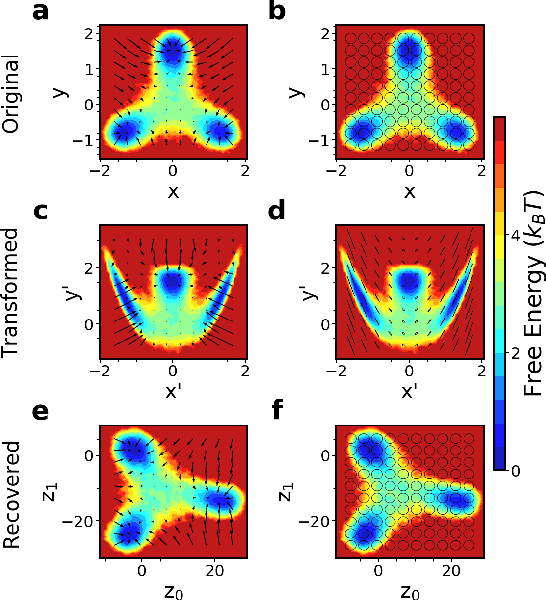
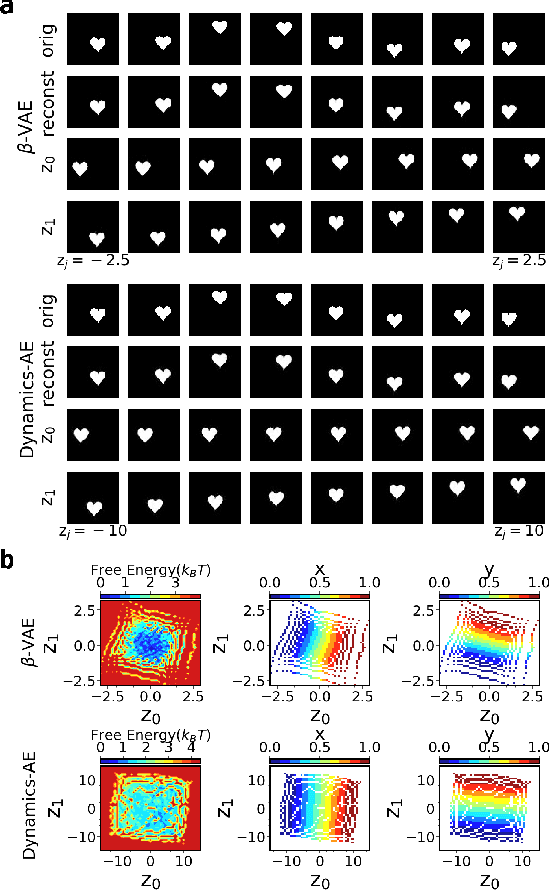
While representation learning has been central to the rise of machine learning and artificial intelligence, a key problem remains in making the learnt representations meaningful. For this the typical approach is to regularize the learned representation through prior probability distributions. However such priors are usually unavailable or ad hoc. To deal with this, we propose a dynamics-constrained representation learning framework. Instead of using predefined probabilities, we restrict the latent representation to follow specific dynamics, which is a more natural constraint for representation learning in dynamical systems. Our belief stems from a fundamental observation in physics that though different systems can have different marginalized probability distributions, they typically obey the same dynamics, such as Newton's and Schrodinger's equations. We validate our framework for different systems including a real-world fluorescent DNA movie dataset. We show that our algorithm can uniquely identify an uncorrelated, isometric and meaningful latent representation.

Thermodynamics of Interpretation

Over the past few years, different types of data-driven Artificial Intelligence (AI) techniques have been widely adopted in various domains of science for generating predictive black-box models. However, because of their black-box nature, it is crucial to establish trust in these models before accepting them as accurate. One way of achieving this goal is through the implementation of a post-hoc interpretation scheme that can put forward the reasons behind a black-box model prediction. In this work, we propose a classical thermodynamics inspired approach for this purpose: Thermodynamically Explainable Representations of AI and other black-box Paradigms (TERP). TERP works by constructing a linear, local surrogate model that approximates the behaviour of the black-box model within a small neighborhood around the instance being explained. By employing a simple forward feature selection Monte Carlo algorithm, TERP assigns an interpretability free energy score to all the possible surrogate models in order to choose an optimal interpretation. Additionally, we validate TERP as a generally applicable method by successfully interpreting four different classes of black-box models trained on datasets coming from relevant domains, including classifying images, predicting heart disease and classifying biomolecular conformations.

Path sampling of recurrent neural networks by incorporating known physics

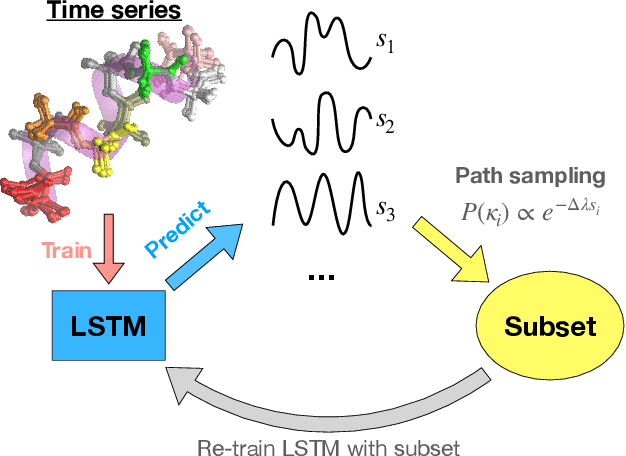
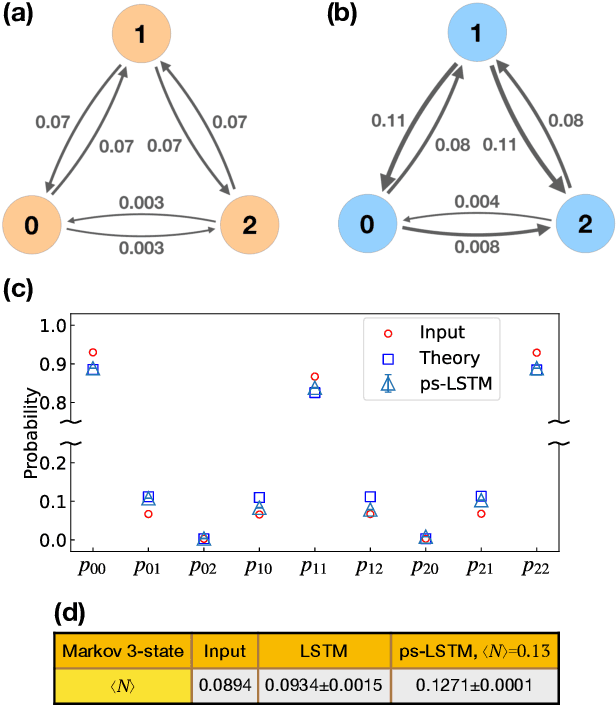
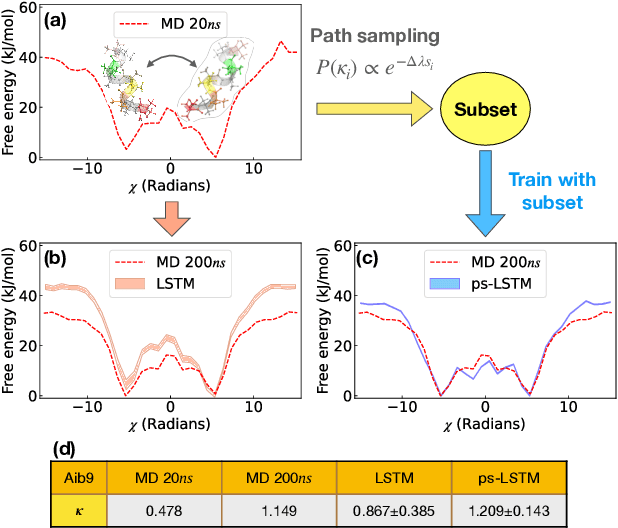
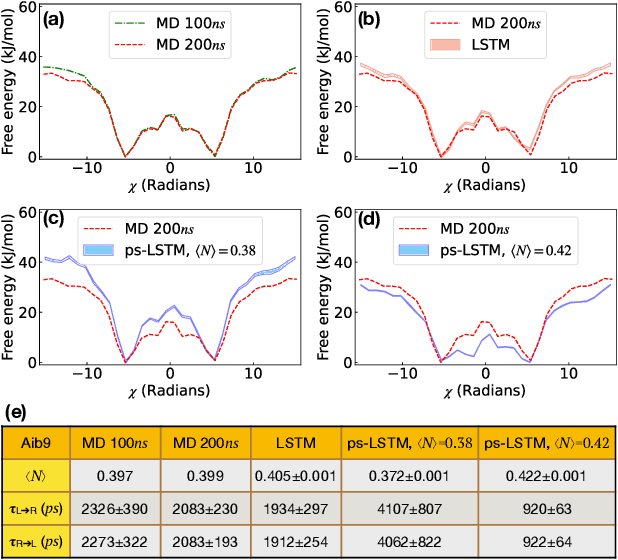
Recurrent neural networks have seen widespread use in modeling dynamical systems in varied domains such as weather prediction, text prediction and several others. Often one wishes to supplement the experimentally observed dynamics with prior knowledge or intuition about the system. While the recurrent nature of these networks allows them to model arbitrarily long memories in the time series used in training, it makes it harder to impose prior knowledge or intuition through generic constraints. In this work, we present a path sampling approach based on principle of Maximum Caliber that allows us to include generic thermodynamic or kinetic constraints into recurrent neural networks. We show the method here for a widely used type of recurrent neural network known as long short-term memory network in the context of supplementing time series collecting from all-atom molecular dynamics. We demonstrate the power of the formalism for different applications. Our method can be easily generalized to other generative artificial intelligence models and to generic time series in different areas of physical and social sciences, where one wishes to supplement limited data with intuition or theory based corrections.