Estimating Vector Fields on Manifolds and the Embedding of Directed Graphs
Paper and Code
May 30, 2014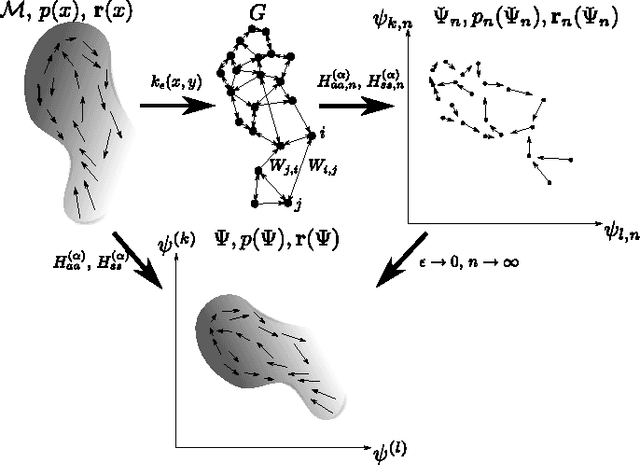
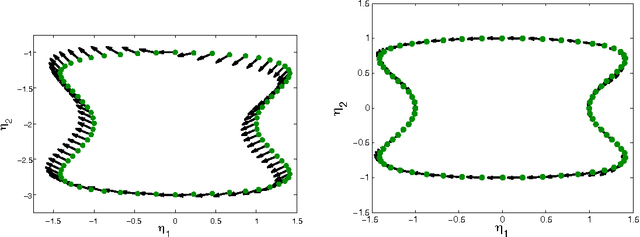

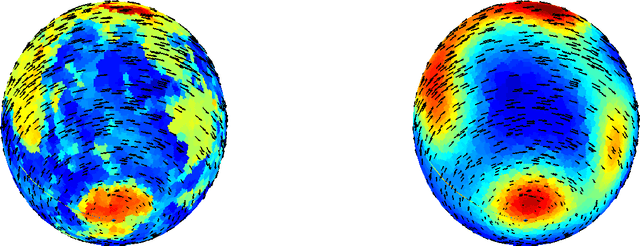
This paper considers the problem of embedding directed graphs in Euclidean space while retaining directional information. We model a directed graph as a finite set of observations from a diffusion on a manifold endowed with a vector field. This is the first generative model of its kind for directed graphs. We introduce a graph embedding algorithm that estimates all three features of this model: the low-dimensional embedding of the manifold, the data density and the vector field. In the process, we also obtain new theoretical results on the limits of "Laplacian type" matrices derived from directed graphs. The application of our method to both artificially constructed and real data highlights its strengths.
* 16 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge