Random Linear Projections Loss for Hyperplane-Based Optimization in Regression Neural Networks

Despite their popularity across a wide range of domains, regression neural networks are prone to overfitting complex datasets. In this work, we propose a loss function termed Random Linear Projections (RLP) loss, which is empirically shown to mitigate overfitting. With RLP loss, the distance between sets of hyperplanes connecting fixed-size subsets of the neural network's feature-prediction pairs and feature-label pairs is minimized. The intuition behind this loss derives from the notion that if two functions share the same hyperplanes connecting all subsets of feature-label pairs, then these functions must necessarily be equivalent. Our empirical studies, conducted across benchmark datasets and representative synthetic examples, demonstrate the improvements of the proposed RLP loss over mean squared error (MSE). Specifically, neural networks trained with the RLP loss achieve better performance while requiring fewer data samples and are more robust to additive noise. We provide theoretical analysis supporting our empirical findings.

Counterfactual Data Augmentation with Contrastive Learning

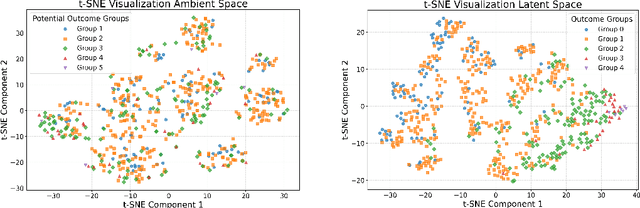
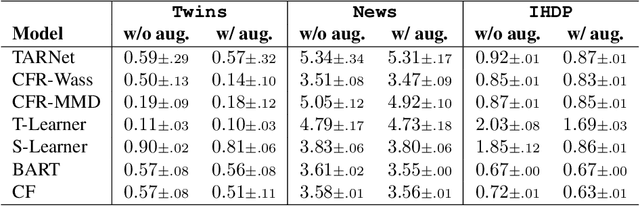
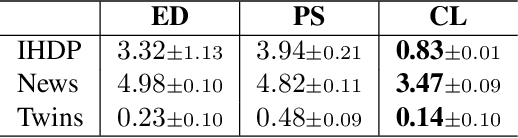
Statistical disparity between distinct treatment groups is one of the most significant challenges for estimating Conditional Average Treatment Effects (CATE). To address this, we introduce a model-agnostic data augmentation method that imputes the counterfactual outcomes for a selected subset of individuals. Specifically, we utilize contrastive learning to learn a representation space and a similarity measure such that in the learned representation space close individuals identified by the learned similarity measure have similar potential outcomes. This property ensures reliable imputation of counterfactual outcomes for the individuals with close neighbors from the alternative treatment group. By augmenting the original dataset with these reliable imputations, we can effectively reduce the discrepancy between different treatment groups, while inducing minimal imputation error. The augmented dataset is subsequently employed to train CATE estimation models. Theoretical analysis and experimental studies on synthetic and semi-synthetic benchmarks demonstrate that our method achieves significant improvements in both performance and robustness to overfitting across state-of-the-art models.

Individual Treatment Effects in Extreme Regimes

Understanding individual treatment effects in extreme regimes is important for characterizing risks associated with different interventions. This is hindered by the fact that extreme regime data may be hard to collect, as it is scarcely observed in practice. In addressing this issue, we propose a new framework for estimating the individual treatment effect in extreme regimes (ITE$_2$). Specifically, we quantify this effect by the changes in the tail decay rates of potential outcomes in the presence or absence of the treatment. Subsequently, we establish conditions under which ITE$_2$ may be calculated and develop algorithms for its computation. We demonstrate the efficacy of our proposed method on various synthetic and semi-synthetic datasets.

Causal Mediation Analysis with Multi-dimensional and Indirectly Observed Mediators

Causal mediation analysis (CMA) is a powerful method to dissect the total effect of a treatment into direct and mediated effects within the potential outcome framework. This is important in many scientific applications to identify the underlying mechanisms of a treatment effect. However, in many scientific applications the mediator is unobserved, but there may exist related measurements. For example, we may want to identify how changes in brain activity or structure mediate an antidepressant's effect on behavior, but we may only have access to electrophysiological or imaging brain measurements. To date, most CMA methods assume that the mediator is one-dimensional and observable, which oversimplifies such real-world scenarios. To overcome this limitation, we introduce a CMA framework that can handle complex and indirectly observed mediators based on the identifiable variational autoencoder (iVAE) architecture. We prove that the true joint distribution over observed and latent variables is identifiable with the proposed method. Additionally, our framework captures a disentangled representation of the indirectly observed mediator and yields accurate estimation of the direct and mediated effects in synthetic and semi-synthetic experiments, providing evidence of its potential utility in real-world applications.

Few-Shot Continual Learning for Conditional Generative Adversarial Networks

In few-shot continual learning for generative models, a target mode must be learned with limited samples without adversely affecting the previously learned modes. In this paper, we propose a new continual learning approach for conditional generative adversarial networks (cGAN) based on a new mode-affinity measure for generative modeling. Our measure is entirely based on the cGAN's discriminator and can identify the existing modes that are most similar to the target. Subsequently, we expand the continual learning model by including the target mode using a weighted label derived from those of the closest modes. To prevent catastrophic forgetting, we first generate labeled data samples using the cGAN's generator, and then train the cGAN model for the target mode while memory replaying with the generated data. Our experimental results demonstrate the efficacy of our approach in improving the generation performance over the baselines and the state-of-the-art approaches for various standard datasets while utilizing fewer training samples.

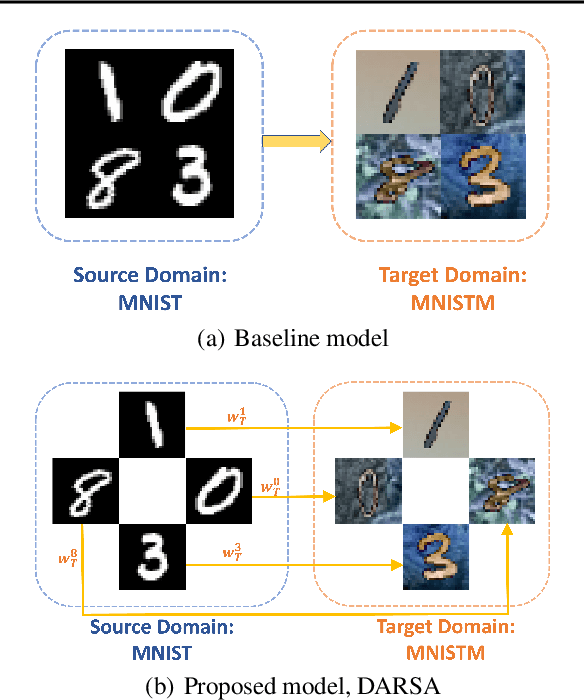
Domain Adaptation via Rebalanced Sub-domain Alignment

Unsupervised domain adaptation (UDA) is a technique used to transfer knowledge from a labeled source domain to a different but related unlabeled target domain. While many UDA methods have shown success in the past, they often assume that the source and target domains must have identical class label distributions, which can limit their effectiveness in real-world scenarios. To address this limitation, we propose a novel generalization bound that reweights source classification error by aligning source and target sub-domains. We prove that our proposed generalization bound is at least as strong as existing bounds under realistic assumptions, and we empirically show that it is much stronger on real-world data. We then propose an algorithm to minimize this novel generalization bound. We demonstrate by numerical experiments that this approach improves performance in shifted class distribution scenarios compared to state-of-the-art methods.

Causal Knowledge Transfer from Task Affinity

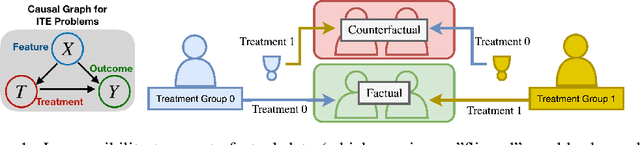
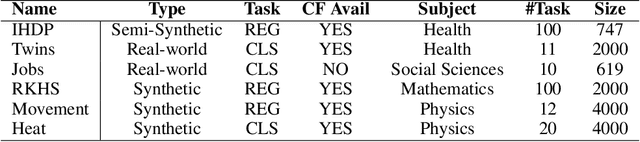
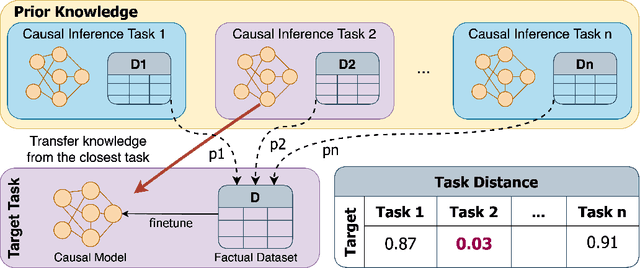
Recent developments in deep representation models through counterfactual balancing have led to a promising framework for estimating Individual Treatment Effects (ITEs) that are essential to causal inference in the Neyman-Rubin potential outcomes framework. While Randomized Control Trials are vital to understanding causal effects, they are sometimes infeasible, costly, or unethical to conduct. Motivated by these potential obstacles to data acquisition, we focus on transferring the causal knowledge acquired in prior experiments to new scenarios for which only limited data is available. To this end, we first observe that the absolute values of ITEs are invariant under the action of the symmetric group on the labels of treatments. Given this invariance, we propose a symmetrized task distance for calculating the similarity of a target scenario with those encountered before. The aforementioned task distance is then used to transfer causal knowledge from the closest of all the available previously learned tasks to the target scenario. We provide upper bounds on the counterfactual loss and ITE error of the target task indicating the transferability of causal knowledge. Empirical studies are provided for various real-world, semi-synthetic, and synthetic datasets demonstrating that the proposed symmetrized task distance is strongly related to the estimation of the counterfactual loss. Numerical results indicate that transferring causal knowledge reduces the amount of required data by up to 95% when compared to training from scratch. These results reveal the promise of our method when applied to important albeit challenging real-world scenarios such as transferring the knowledge of treatment effects (e.g., medicine, social policy, personal training, etc.) studied on a population to other groups absent in the study.