Generalisation of Total Uncertainty in AI: A Theoretical Study

AI has been dealing with uncertainty to have highly accurate results. This becomes even worse with reasonably small data sets or a variation in the data sets. This has far-reaching effects on decision-making, forecasting and learning mechanisms. This study seeks to unpack the nature of uncertainty that exists within AI by drawing ideas from established works, the latest developments and practical applications and provide a novel total uncertainty definition in AI. From inception theories up to current methodologies, this paper provides an integrated view of dealing with better total uncertainty as well as complexities of uncertainty in AI that help us understand its meaning and value across different domains.

Credal Wrapper of Model Averaging for Uncertainty Estimation on Out-Of-Distribution Detection

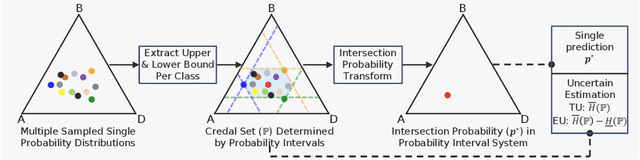
This paper presents an innovative approach, called credal wrapper, to formulating a credal set representation of model averaging for Bayesian neural networks (BNNs) and deep ensembles, capable of improving uncertainty estimation in classification tasks. Given a finite collection of single distributions derived from BNNs or deep ensembles, the proposed approach extracts an upper and a lower probability bound per class, acknowledging the epistemic uncertainty due to the availability of a limited amount of sampled predictive distributions. Such probability intervals over classes can be mapped on a convex set of probabilities (a 'credal set') from which, in turn, a unique prediction can be obtained using a transformation called 'intersection probability transformation'. In this article, we conduct extensive experiments on multiple out-of-distribution (OOD) detection benchmarks, encompassing various dataset pairs (CIFAR10/100 vs SVHN/Tiny-ImageNet, CIFAR10 vs CIFAR10-C, CIFAR100 vs CIFAR100-C and ImageNet vs ImageNet-O) and using different network architectures (such as VGG16, Res18/50, EfficientNet B2, and ViT Base). Compared to BNN and deep ensemble baselines, the proposed credal representation methodology exhibits superior performance in uncertainty estimation and achieves lower expected calibration error on OOD samples.

CreINNs: Credal-Set Interval Neural Networks for Uncertainty Estimation in Classification Tasks

Uncertainty estimation is increasingly attractive for improving the reliability of neural networks. In this work, we present novel credal-set interval neural networks (CreINNs) designed for classification tasks. CreINNs preserve the traditional interval neural network structure, capturing weight uncertainty through deterministic intervals, while forecasting credal sets using the mathematical framework of probability intervals. Experimental validations on an out-of-distribution detection benchmark (CIFAR10 vs SVHN) showcase that CreINNs outperform epistemic uncertainty estimation when compared to variational Bayesian neural networks (BNNs) and deep ensembles (DEs). Furthermore, CreINNs exhibit a notable reduction in computational complexity compared to variational BNNs and demonstrate smaller model sizes than DEs.

Random-Set Convolutional Neural Network (RS-CNN) for Epistemic Deep Learning

Machine learning is increasingly deployed in safety-critical domains where robustness against adversarial attacks is crucial and erroneous predictions could lead to potentially catastrophic consequences. This highlights the need for learning systems to be equipped with the means to determine a model's confidence in its prediction and the epistemic uncertainty associated with it, 'to know when a model does not know'. In this paper, we propose a novel Random-Set Convolutional Neural Network (RS-CNN) for classification which predicts belief functions rather than probability vectors over the set of classes, using the mathematics of random sets, i.e., distributions over the power set of the sample space. Based on the epistemic deep learning approach, random-set models are capable of representing the 'epistemic' uncertainty induced in machine learning by limited training sets. We estimate epistemic uncertainty by approximating the size of credal sets associated with the predicted belief functions, and experimentally demonstrate how our approach outperforms competing uncertainty-aware approaches in a classical evaluation setting. The performance of RS-CNN is best demonstrated on OOD samples where it manages to capture the true prediction while standard CNNs fail.

An introduction to optimization under uncertainty -- A short survey

Optimization equips engineers and scientists in a variety of fields with the ability to transcribe their problems into a generic formulation and receive optimal solutions with relative ease. Industries ranging from aerospace to robotics continue to benefit from advancements in optimization theory and the associated algorithmic developments. Nowadays, optimization is used in real time on autonomous systems acting in safety critical situations, such as self-driving vehicles. It has become increasingly more important to produce robust solutions by incorporating uncertainty into optimization programs. This paper provides a short survey about the state of the art in optimization under uncertainty. The paper begins with a brief overview of the main classes of optimization without uncertainty. The rest of the paper focuses on the different methods for handling both aleatoric and epistemic uncertainty. Many of the applications discussed in this paper are within the domain of control. The goal of this survey paper is to briefly touch upon the state of the art in a variety of different methods and refer the reader to other literature for more in-depth treatments of the topics discussed here.

Path Planning Problem under non-probabilistic Uncertainty

This paper considers theoretical solutions for path planning problems under non-probabilistic uncertainty used in the travel salesman problems under uncertainty. The uncertainty is on the paths between the cities as nodes in a travelling salesman problem. There is at least one path between two nodes/stations where the travelling time between the nodes is not precisely known. This could be due to environmental effects like crowdedness (rush period) in the path, the state of the charge of batteries, weather conditions, or considering the safety of the route while travelling. In this work, we consider two different advanced uncertainty models (i) probabilistic-precise uncertain model: Probability distributions and (ii) non-probabilistic--imprecise uncertain model: Intervals. We investigate what theoretical results can be obtained for two different optimality criteria: maximinity and maximality in the travelling salesman problem.