Identifiability of latent causal graphical models without pure children

This paper considers a challenging problem of identifying a causal graphical model under the presence of latent variables. While various identifiability conditions have been proposed in the literature, they often require multiple pure children per latent variable or restrictions on the latent causal graph. Furthermore, it is common for all observed variables to exhibit the same modality. Consequently, the existing identifiability conditions are often too stringent for complex real-world data. We consider a general nonparametric measurement model with arbitrary observed variable types and binary latent variables, and propose a double triangular graphical condition that guarantees identifiability of the entire causal graphical model. The proposed condition significantly relaxes the popular pure children condition. We also establish necessary conditions for identifiability and provide valuable insights into fundamental limits of identifiability. Simulation studies verify that latent structures satisfying our conditions can be accurately estimated from data.

Minimax-Optimal Dimension-Reduced Clustering for High-Dimensional Nonspherical Mixtures

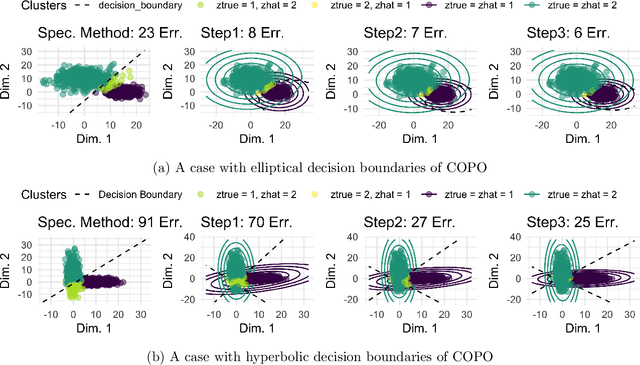
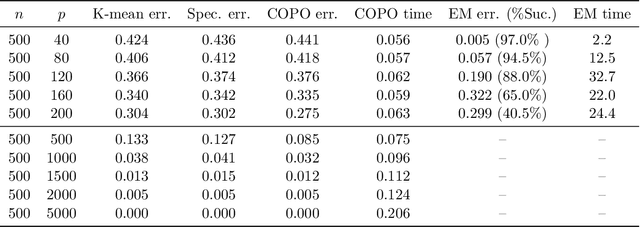
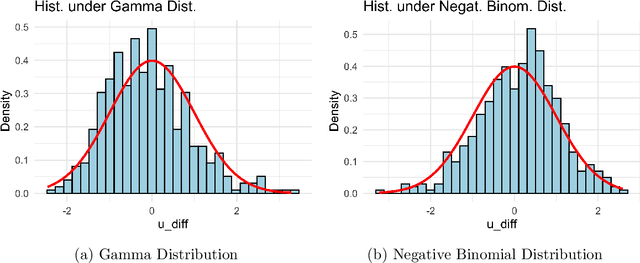
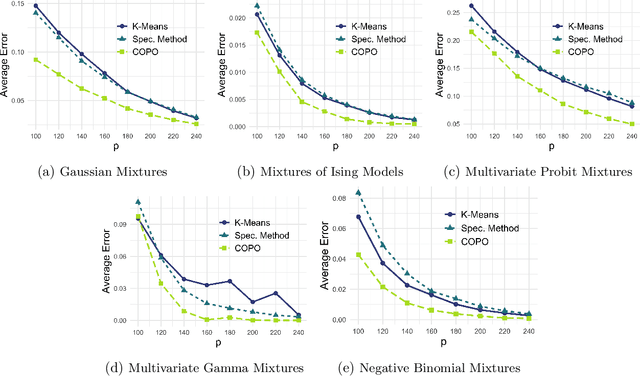
In mixture models, nonspherical (anisotropic) noise within each cluster is widely present in real-world data. We study both the minimax rate and optimal statistical procedure for clustering under high-dimensional nonspherical mixture models. In high-dimensional settings, we first establish the information-theoretic limits for clustering under Gaussian mixtures. The minimax lower bound unveils an intriguing informational dimension-reduction phenomenon: there exists a substantial gap between the minimax rate and the oracle clustering risk, with the former determined solely by the projected centers and projected covariance matrices in a low-dimensional space. Motivated by the lower bound, we propose a novel computationally efficient clustering method: Covariance Projected Spectral Clustering (COPO). Its key step is to project the high-dimensional data onto the low-dimensional space spanned by the cluster centers and then use the projected covariance matrices in this space to enhance clustering. We establish tight algorithmic upper bounds for COPO, both for Gaussian noise with flexible covariance and general noise with local dependence. Our theory indicates the minimax-optimality of COPO in the Gaussian case and highlights its adaptivity to a broad spectrum of dependent noise. Extensive simulation studies under various noise structures and real data analysis demonstrate our method's superior performance.

Minimax-Optimal Covariance Projected Spectral Clustering for High-Dimensional Nonspherical Mixtures

In mixture models, nonspherical (anisotropic) noise within each cluster is widely present in real-world data. We study both the minimax rate and optimal statistical procedure for clustering under high-dimensional nonspherical mixture models. In high-dimensional settings, we first establish the information-theoretic limits for clustering under Gaussian mixtures. The minimax lower bound unveils an intriguing informational dimension-reduction phenomenon: there exists a substantial gap between the minimax rate and the oracle clustering risk, with the former determined solely by the projected centers and projected covariance matrices in a low-dimensional space. Motivated by the lower bound, we propose a novel computationally efficient clustering method: Covariance Projected Spectral Clustering (COPO). Its key step is to project the high-dimensional data onto the low-dimensional space spanned by the cluster centers and then use the projected covariance matrices in this space to enhance clustering. We establish tight algorithmic upper bounds for COPO, both for Gaussian noise with flexible covariance and general noise with local dependence. Our theory indicates the minimax-optimality of COPO in the Gaussian case and highlights its adaptivity to a broad spectrum of dependent noise. Extensive simulation studies under various noise structures and real data analysis demonstrate our method's superior performance.

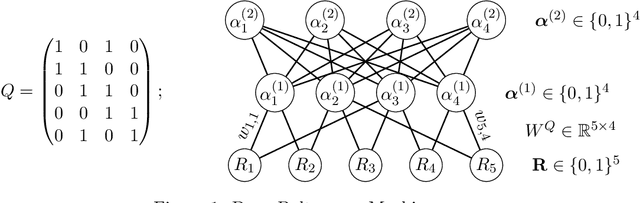
Unfolding Tensors to Identify the Graph in Discrete Latent Bipartite Graphical Models

We use a tensor unfolding technique to prove a new identifiability result for discrete bipartite graphical models, which have a bipartite graph between an observed and a latent layer. This model family includes popular models such as Noisy-Or Bayesian networks for medical diagnosis and Restricted Boltzmann Machines in machine learning. These models are also building blocks for deep generative models. Our result on identifying the graph structure enjoys the following nice properties. First, our identifiability proof is constructive, in which we innovatively unfold the population tensor under the model into matrices and inspect the rank properties of the resulting matrices to uncover the graph. This proof itself gives a population-level structure learning algorithm that outputs both the number of latent variables and the bipartite graph. Second, we allow various forms of nonlinear dependence among the variables, unlike many continuous latent variable graphical models that rely on linearity to show identifiability. Third, our identifiability condition is interpretable, only requiring each latent variable to connect to at least two "pure" observed variables in the bipartite graph. The new result not only brings novel advances in algebraic statistics, but also has useful implications for these models' trustworthy applications in scientific disciplines and interpretable machine learning.

Deep Discrete Encoders: Identifiable Deep Generative Models for Rich Data with Discrete Latent Layers

In the era of generative AI, deep generative models (DGMs) with latent representations have gained tremendous popularity. Despite their impressive empirical performance, the statistical properties of these models remain underexplored. DGMs are often overparametrized, non-identifiable, and uninterpretable black boxes, raising serious concerns when deploying them in high-stakes applications. Motivated by this, we propose an interpretable deep generative modeling framework for rich data types with discrete latent layers, called Deep Discrete Encoders (DDEs). A DDE is a directed graphical model with multiple binary latent layers. Theoretically, we propose transparent identifiability conditions for DDEs, which imply progressively smaller sizes of the latent layers as they go deeper. Identifiability ensures consistent parameter estimation and inspires an interpretable design of the deep architecture. Computationally, we propose a scalable estimation pipeline of a layerwise nonlinear spectral initialization followed by a penalized stochastic approximation EM algorithm. This procedure can efficiently estimate models with exponentially many latent components. Extensive simulation studies validate our theoretical results and demonstrate the proposed algorithms' excellent performance. We apply DDEs to three diverse real datasets for hierarchical topic modeling, image representation learning, response time modeling in educational testing, and obtain interpretable findings.

Generalized Grade-of-Membership Estimation for High-dimensional Locally Dependent Data

This work focuses on the mixed membership models for multivariate categorical data widely used for analyzing survey responses and population genetics data. These grade of membership (GoM) models offer rich modeling power but present significant estimation challenges for high-dimensional polytomous data. Popular existing approaches, such as Bayesian MCMC inference, are not scalable and lack theoretical guarantees in high-dimensional settings. To address this, we first observe that data from this model can be reformulated as a three-way (quasi-)tensor, with many subjects responding to many items with varying numbers of categories. We introduce a novel and simple approach that flattens the three-way quasi-tensor into a "fat" matrix, and then perform a singular value decomposition of it to estimate parameters by exploiting the singular subspace geometry. Our fast spectral method can accommodate a broad range of data distributions with arbitrarily locally dependent noise, which we formalize as the generalized-GoM models. We establish finite-sample entrywise error bounds for the generalized-GoM model parameters. This is supported by a new sharp two-to-infinity singular subspace perturbation theory for locally dependent and flexibly distributed noise, a contribution of independent interest. Simulations and applications to data in political surveys, population genetics, and single-cell sequencing demonstrate our method's superior performance.

Adaptive Transfer Clustering: A Unified Framework

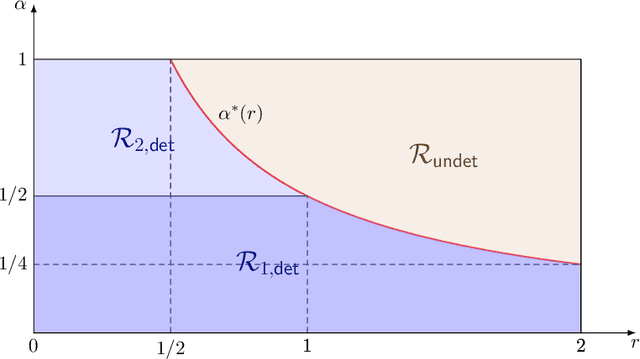
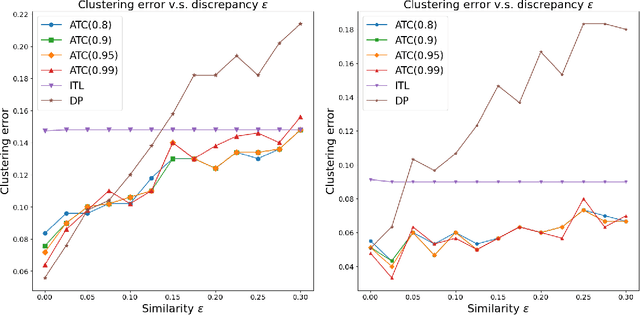
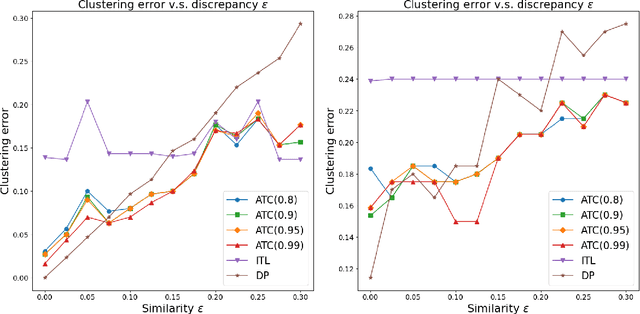
We propose a general transfer learning framework for clustering given a main dataset and an auxiliary one about the same subjects. The two datasets may reflect similar but different latent grouping structures of the subjects. We propose an adaptive transfer clustering (ATC) algorithm that automatically leverages the commonality in the presence of unknown discrepancy, by optimizing an estimated bias-variance decomposition. It applies to a broad class of statistical models including Gaussian mixture models, stochastic block models, and latent class models. A theoretical analysis proves the optimality of ATC under the Gaussian mixture model and explicitly quantifies the benefit of transfer. Extensive simulations and real data experiments confirm our method's effectiveness in various scenarios.

Learning from Similar Linear Representations: Adaptivity, Minimaxity, and Robustness

Representation multi-task learning (MTL) and transfer learning (TL) have achieved tremendous success in practice. However, the theoretical understanding of these methods is still lacking. Most existing theoretical works focus on cases where all tasks share the same representation, and claim that MTL and TL almost always improve performance. However, as the number of tasks grow, assuming all tasks share the same representation is unrealistic. Also, this does not always match empirical findings, which suggest that a shared representation may not necessarily improve single-task or target-only learning performance. In this paper, we aim to understand how to learn from tasks with \textit{similar but not exactly the same} linear representations, while dealing with outlier tasks. We propose two algorithms that are \textit{adaptive} to the similarity structure and \textit{robust} to outlier tasks under both MTL and TL settings. Our algorithms outperform single-task or target-only learning when representations across tasks are sufficiently similar and the fraction of outlier tasks is small. Furthermore, they always perform no worse than single-task learning or target-only learning, even when the representations are dissimilar. We provide information-theoretic lower bounds to show that our algorithms are nearly \textit{minimax} optimal in a large regime.

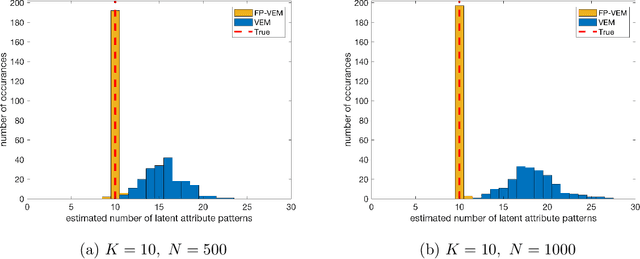
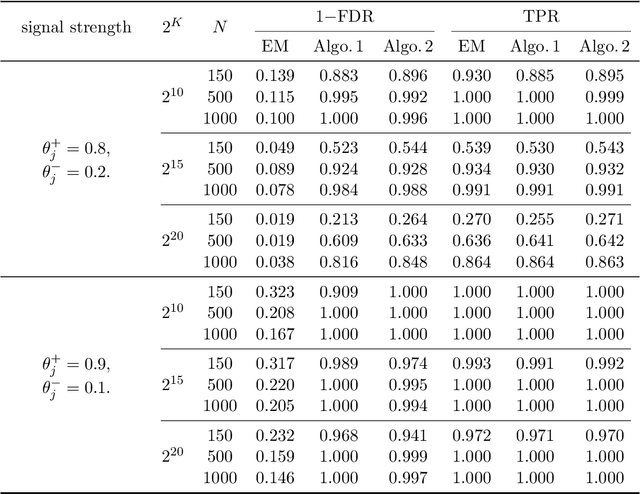
Identification and Estimation of Hierarchical Latent Attribute Models

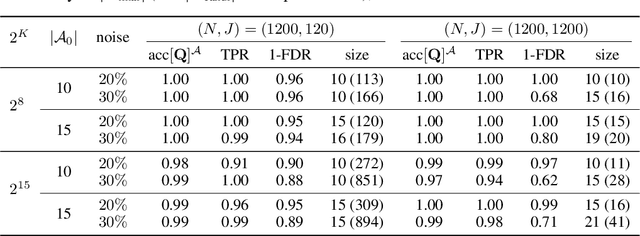
Hierarchical Latent Attribute Models (HLAMs) are a popular family of discrete latent variable models widely used in social and biological sciences. The key ingredients of an HLAM include a binary structural matrix specifying how the observed variables depend on the latent attributes, and also certain hierarchical constraints on allowable configurations of the latent attributes. This paper studies the theoretical identifiability issue and the practical estimation problem of HLAMs. For identification, the challenging problem of identifiability under a complex hierarchy is addressed and sufficient and almost necessary identification conditions are proposed. For estimation, a scalable algorithm for estimating both the structural matrix and the attribute hierarchy is developed. The superior performance of the proposed algorithm is demonstrated in various experimental settings, including both synthetic data and a real dataset from an international educational assessment.

Learning Attribute Patterns in High-Dimensional Structured Latent Attribute Models

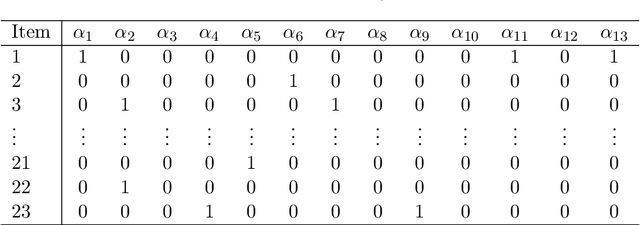
Structured latent attribute models (SLAMs) are a special family of discrete latent variable models widely used in social and biological sciences. This paper considers the problem of learning significant attribute patterns from a SLAM with potentially high-dimensional configurations of the latent attributes. We address the theoretical identifiability issue, propose a penalized likelihood method for the selection of the attribute patterns, and further establish the selection consistency in such an overfitted SLAM with diverging number of latent patterns. The good performance of the proposed methodology is illustrated by simulation studies and two real datasets in educational assessment.