tinyBenchmarks: evaluating LLMs with fewer examples

The versatility of large language models (LLMs) led to the creation of diverse benchmarks that thoroughly test a variety of language models' abilities. These benchmarks consist of tens of thousands of examples making evaluation of LLMs very expensive. In this paper, we investigate strategies to reduce the number of evaluations needed to assess the performance of an LLM on several key benchmarks. For example, we show that to accurately estimate the performance of an LLM on MMLU, a popular multiple-choice QA benchmark consisting of 14K examples, it is sufficient to evaluate this LLM on 100 curated examples. We release evaluation tools and tiny versions of popular benchmarks: Open LLM Leaderboard, MMLU, HELM, and AlpacaEval 2.0. Our empirical analysis demonstrates that these tools and tiny benchmarks are sufficient to reliably and efficiently reproduce the original evaluation results.

Learning Latent and Hierarchical Structures in Cognitive Diagnosis Models

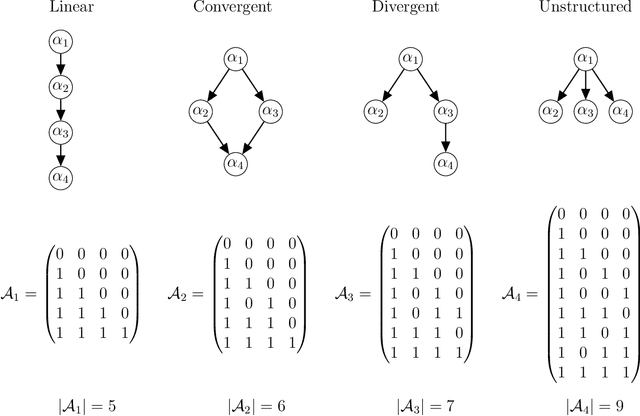
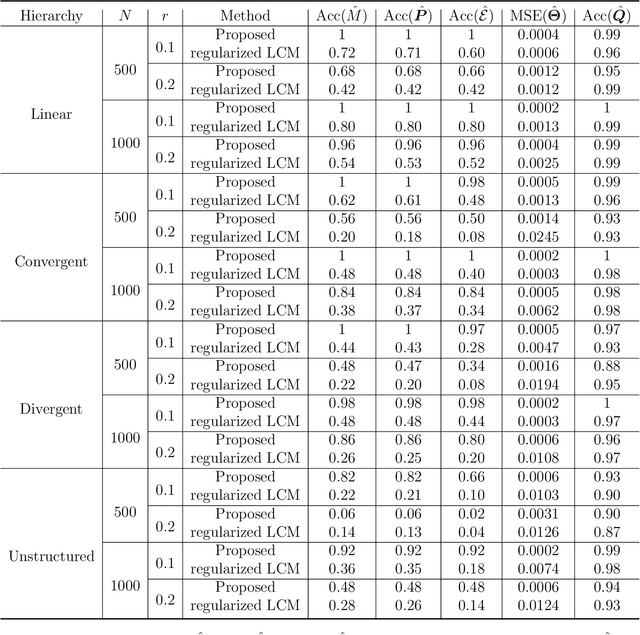
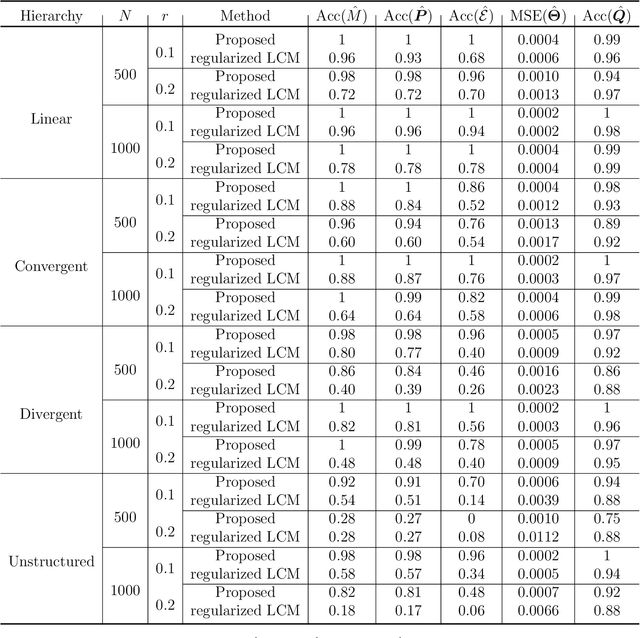
Cognitive Diagnosis Models (CDMs) are a special family of discrete latent variable models that are widely used in modern educational, psychological, social and biological sciences. A key component of CDMs is a binary $Q$-matrix characterizing the dependence structure between the items and the latent attributes. Additionally, researchers also assume in many applications certain hierarchical structures among the latent attributes to characterize their dependence. In most CDM applications, the attribute-attribute hierarchical structures, the item-attribute $Q$-matrix, the item-level diagnostic model, as well as the number of latent attributes, need to be fully or partially pre-specified, which however may be subjective and misspecified as noted by many recent studies. This paper considers the problem of jointly learning these latent and hierarchical structures in CDMs from observed data with minimal model assumptions. Specifically, a penalized likelihood approach is proposed to select the number of attributes and estimate the latent and hierarchical structures simultaneously. An efficient expectation-maximization (EM) algorithm and a latent structure recovery algorithm are developed, and statistical consistency theory is also established under mild conditions. The good performance of the proposed method is illustrated by simulation studies and a real data application in educational assessment.

Identification and Estimation of Hierarchical Latent Attribute Models

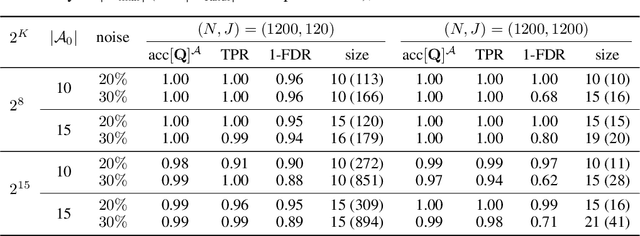
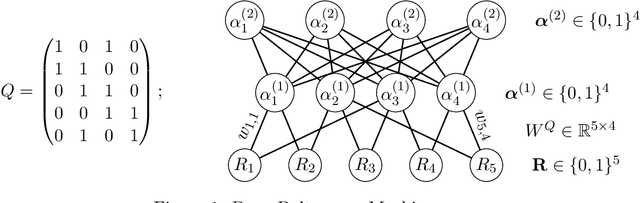
Hierarchical Latent Attribute Models (HLAMs) are a popular family of discrete latent variable models widely used in social and biological sciences. The key ingredients of an HLAM include a binary structural matrix specifying how the observed variables depend on the latent attributes, and also certain hierarchical constraints on allowable configurations of the latent attributes. This paper studies the theoretical identifiability issue and the practical estimation problem of HLAMs. For identification, the challenging problem of identifiability under a complex hierarchy is addressed and sufficient and almost necessary identification conditions are proposed. For estimation, a scalable algorithm for estimating both the structural matrix and the attribute hierarchy is developed. The superior performance of the proposed algorithm is demonstrated in various experimental settings, including both synthetic data and a real dataset from an international educational assessment.

Learning Attribute Patterns in High-Dimensional Structured Latent Attribute Models

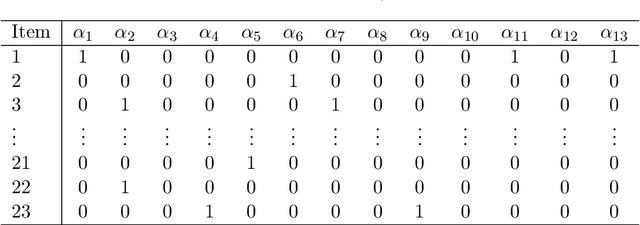
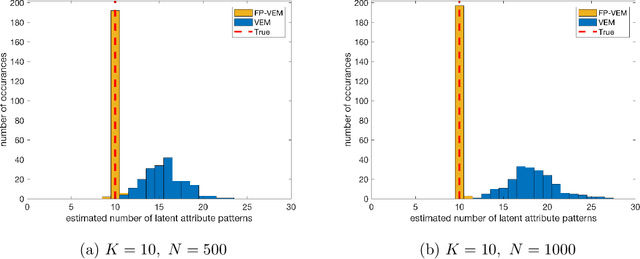
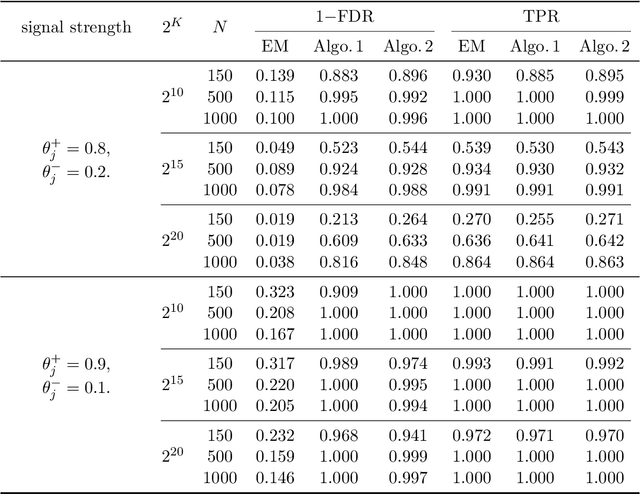
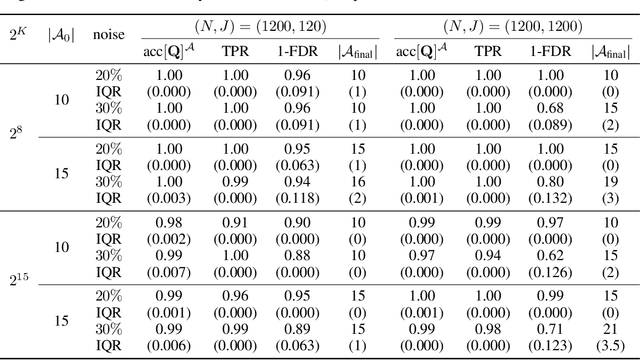
Structured latent attribute models (SLAMs) are a special family of discrete latent variable models widely used in social and biological sciences. This paper considers the problem of learning significant attribute patterns from a SLAM with potentially high-dimensional configurations of the latent attributes. We address the theoretical identifiability issue, propose a penalized likelihood method for the selection of the attribute patterns, and further establish the selection consistency in such an overfitted SLAM with diverging number of latent patterns. The good performance of the proposed methodology is illustrated by simulation studies and two real datasets in educational assessment.