Learning Attribute Patterns in High-Dimensional Structured Latent Attribute Models
Paper and Code
Apr 08, 2019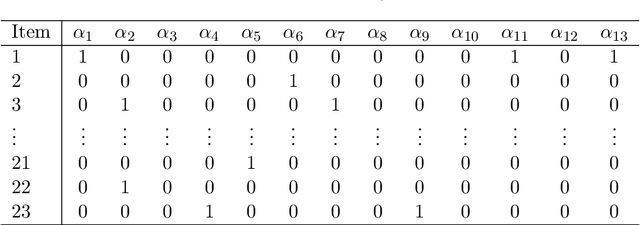
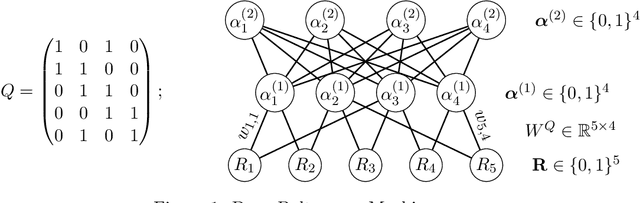
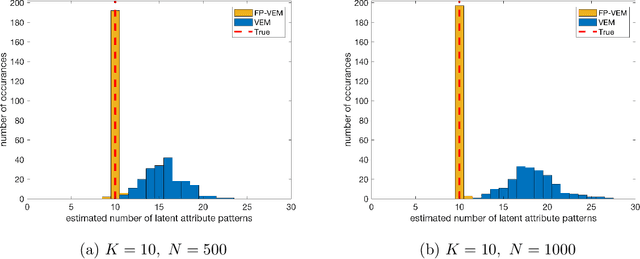
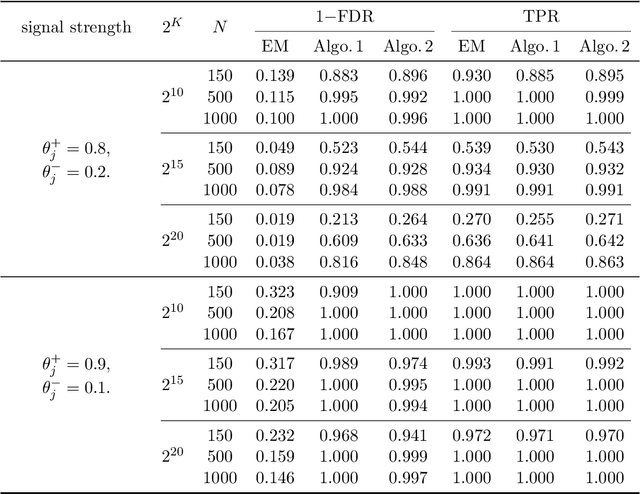
Structured latent attribute models (SLAMs) are a special family of discrete latent variable models widely used in social and biological sciences. This paper considers the problem of learning significant attribute patterns from a SLAM with potentially high-dimensional configurations of the latent attributes. We address the theoretical identifiability issue, propose a penalized likelihood method for the selection of the attribute patterns, and further establish the selection consistency in such an overfitted SLAM with diverging number of latent patterns. The good performance of the proposed methodology is illustrated by simulation studies and two real datasets in educational assessment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge