Choquet regularization for reinforcement learning

We propose \emph{Choquet regularizers} to measure and manage the level of exploration for reinforcement learning (RL), and reformulate the continuous-time entropy-regularized RL problem of Wang et al. (2020, JMLR, 21(198)) in which we replace the differential entropy used for regularization with a Choquet regularizer. We derive the Hamilton--Jacobi--Bellman equation of the problem, and solve it explicitly in the linear--quadratic (LQ) case via maximizing statically a mean--variance constrained Choquet regularizer. Under the LQ setting, we derive explicit optimal distributions for several specific Choquet regularizers, and conversely identify the Choquet regularizers that generate a number of broadly used exploratory samplers such as $\epsilon$-greedy, exponential, uniform and Gaussian.

A unified framework for bandit multiple testing

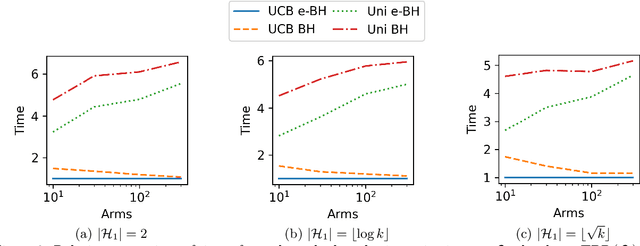
In bandit multiple hypothesis testing, each arm corresponds to a different null hypothesis that we wish to test, and the goal is to design adaptive algorithms that correctly identify large set of interesting arms (true discoveries), while only mistakenly identifying a few uninteresting ones (false discoveries). One common metric in non-bandit multiple testing is the false discovery rate (FDR). We propose a unified, modular framework for bandit FDR control that emphasizes the decoupling of exploration and summarization of evidence. We utilize the powerful martingale-based concept of ``e-processes'' to ensure FDR control for arbitrary composite nulls, exploration rules and stopping times in generic problem settings. In particular, valid FDR control holds even if the reward distributions of the arms could be dependent, multiple arms may be queried simultaneously, and multiple (cooperating or competing) agents may be querying arms, covering combinatorial semi-bandit type settings as well. Prior work has considered in great detail the setting where each arm's reward distribution is independent and sub-Gaussian, and a single arm is queried at each step. Our framework recovers matching sample complexity guarantees in this special case, and performs comparably or better in practice. For other settings, sample complexities will depend on the finer details of the problem (composite nulls being tested, exploration algorithm, data dependence structure, stopping rule) and we do not explore these; our contribution is to show that the FDR guarantee is clean and entirely agnostic to these details.