Reinforcement Learning for Jump-Diffusions

We study continuous-time reinforcement learning (RL) for stochastic control in which system dynamics are governed by jump-diffusion processes. We formulate an entropy-regularized exploratory control problem with stochastic policies to capture the exploration--exploitation balance essential for RL. Unlike the pure diffusion case initially studied by Wang et al. (2020), the derivation of the exploratory dynamics under jump-diffusions calls for a careful formulation of the jump part. Through a theoretical analysis, we find that one can simply use the same policy evaluation and q-learning algorithms in Jia and Zhou (2022a, 2023), originally developed for controlled diffusions, without needing to check a priori whether the underlying data come from a pure diffusion or a jump-diffusion. However, we show that the presence of jumps ought to affect parameterizations of actors and critics in general. Finally, we investigate as an application the mean-variance portfolio selection problem with stock price modelled as a jump-diffusion, and show that both RL algorithms and parameterizations are invariant with respect to jumps.

Data-driven Hedging of Stock Index Options via Deep Learning

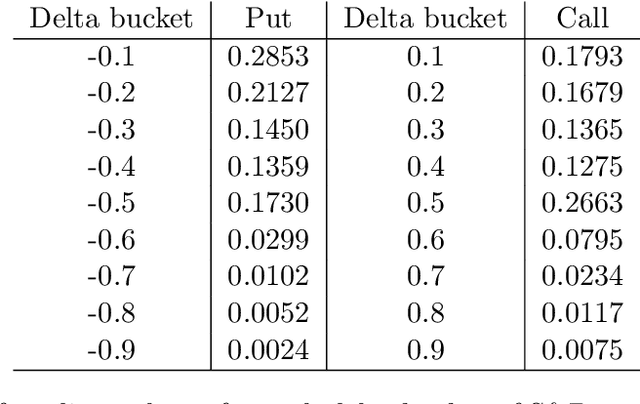
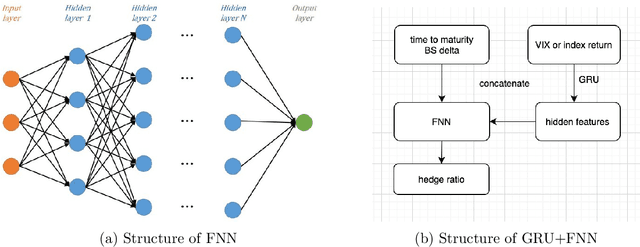
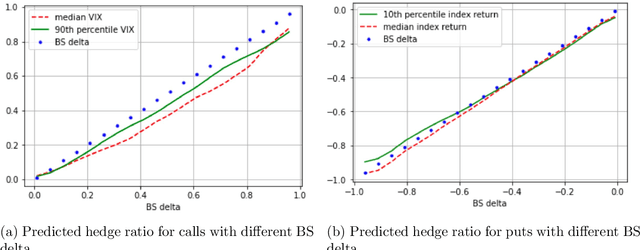
We develop deep learning models to learn the hedge ratio for S&P500 index options directly from options data. We compare different combinations of features and show that a feedforward neural network model with time to maturity, Black-Scholes delta and a sentiment variable (VIX for calls and index return for puts) as input features performs the best in the out-of-sample test. This model significantly outperforms the standard hedging practice that uses the Black-Scholes delta and a recent data-driven model. Our results demonstrate the importance of market sentiment for hedging efficiency, a factor previously ignored in developing hedging strategies.