Convergence and Regret of the Policy Gradient for Multi-Armed Bandits in Diffusion Environment

This paper studies the policy gradient update for a multi-arm bandit problem in diffusion environment that is described by a stochastic differential equation (SDE) under the continuous-time reinforcement learning framework by Wang et al. (2020), Jia and Zhou (2022b). With the logit parameterization for the stochastic policy, we show that it converges almost surely to the optimal arm under an arbitrary constant learning rate. Furthermore, we derive the non-asymptotic regret upper bound when the constant learning rate is below a time-invariant threshold; and the regret bound has order $O(\log T)$. We improve the analysis in Lattimore (2026a) for the same SDE by constructing a novel Lyapunov function and demonstrate the transparency of analyzing policy gradient using the tools in SDEs. In addition, the same Lyapunov function is also helpful in analyzing the discrete-time policy gradient algorithm.

A Zeroth-Order Deep Learning Method for Fully Nonlinear Parabolic Partial Differential Equations with Unknown Coefficients

High-dimensional partial differential equations (PDEs) with unknown coefficients arise widely in scientific machine learning, including continuous-time reinforcement learning, yet solving them efficiently in a data-driven way remains challenging. Existing deep learning solvers often rely on repeated automatic differentiation to evaluate differential operators, which can cause instability and amplify derivative errors in high dimensions, while probabilistic methods based on stochastic representations require explicit knowledge of the data-generating dynamics and therefore do not apply to black-box environments. We introduce two types of simulators as data-generating mechanisms, and take a ``representing-then-learning" approach that learns the solutions and their derivatives under settings where the underlying PDE operators are accessible only through simulations and pointwise evaluations. Our representation of derivatives relies on the zeroth-order derivative (ZOD) estimators derived from perturbed Monte Carlo trajectories. This fully model-free approach generates targets for the gradient and Hessian networks using only function evaluations. We provide a statistical learning analysis of the proposed approach, including a bias--variance tradeoff for ZODs. Assuming a standard contraction property of the underlying operator, we establish a non-asymptotic error bound that decomposes the total error into discretization error, approximation error, statistical error, and ZOD bias. Crucially, we derive the sample complexity of the learned representations in (weighted) Sobolev space, characterizing the error up to second-order derivatives. Numerical experiments illustrate the competitive performance of the method in moderate and high dimensions.

Accuracy of Discretely Sampled Stochastic Policies in Continuous-time Reinforcement Learning

Stochastic policies are widely used in continuous-time reinforcement learning algorithms. However, executing a stochastic policy and evaluating its performance in a continuous-time environment remain open challenges. This work introduces and rigorously analyzes a policy execution framework that samples actions from a stochastic policy at discrete time points and implements them as piecewise constant controls. We prove that as the sampling mesh size tends to zero, the controlled state process converges weakly to the dynamics with coefficients aggregated according to the stochastic policy. We explicitly quantify the convergence rate based on the regularity of the coefficients and establish an optimal first-order convergence rate for sufficiently regular coefficients. Additionally, we show that the same convergence rates hold with high probability concerning the sampling noise, and further establish a $1/2$-order almost sure convergence when the volatility is not controlled. Building on these results, we analyze the bias and variance of various policy evaluation and policy gradient estimators based on discrete-time observations. Our results provide theoretical justification for the exploratory stochastic control framework in [H. Wang, T. Zariphopoulou, and X.Y. Zhou, J. Mach. Learn. Res., 21 (2020), pp. 1-34].

Sublinear Regret for An Actor-Critic Algorithm in Continuous-Time Linear-Quadratic Reinforcement Learning

We study reinforcement learning (RL) for a class of continuous-time linear-quadratic (LQ) control problems for diffusions where volatility of the state processes depends on both state and control variables. We apply a model-free approach that relies neither on knowledge of model parameters nor on their estimations, and devise an actor-critic algorithm to learn the optimal policy parameter directly. Our main contributions include the introduction of a novel exploration schedule and a regret analysis of the proposed algorithm. We provide the convergence rate of the policy parameter to the optimal one, and prove that the algorithm achieves a regret bound of $O(N^{\frac{3}{4}})$ up to a logarithmic factor. We conduct a simulation study to validate the theoretical results and demonstrate the effectiveness and reliability of the proposed algorithm. We also perform numerical comparisons between our method and those of the recent model-based stochastic LQ RL studies adapted to the state- and control-dependent volatility setting, demonstrating a better performance of the former in terms of regret bounds.

Continuous-time Risk-sensitive Reinforcement Learning via Quadratic Variation Penalty

This paper studies continuous-time risk-sensitive reinforcement learning (RL) under the entropy-regularized, exploratory diffusion process formulation with the exponential-form objective. The risk-sensitive objective arises either as the agent's risk attitude or as a distributionally robust approach against the model uncertainty. Owing to the martingale perspective in Jia and Zhou (2023) the risk-sensitive RL problem is shown to be equivalent to ensuring the martingale property of a process involving both the value function and the q-function, augmented by an additional penalty term: the quadratic variation of the value process, capturing the variability of the value-to-go along the trajectory. This characterization allows for the straightforward adaptation of existing RL algorithms developed for non-risk-sensitive scenarios to incorporate risk sensitivity by adding the realized variance of the value process. Additionally, I highlight that the conventional policy gradient representation is inadequate for risk-sensitive problems due to the nonlinear nature of quadratic variation; however, q-learning offers a solution and extends to infinite horizon settings. Finally, I prove the convergence of the proposed algorithm for Merton's investment problem and quantify the impact of temperature parameter on the behavior of the learning procedure. I also conduct simulation experiments to demonstrate how risk-sensitive RL improves the finite-sample performance in the linear-quadratic control problem.

Learning Merton's Strategies in an Incomplete Market: Recursive Entropy Regularization and Biased Gaussian Exploration

We study Merton's expected utility maximization problem in an incomplete market, characterized by a factor process in addition to the stock price process, where all the model primitives are unknown. We take the reinforcement learning (RL) approach to learn optimal portfolio policies directly by exploring the unknown market, without attempting to estimate the model parameters. Based on the entropy-regularization framework for general continuous-time RL formulated in Wang et al. (2020), we propose a recursive weighting scheme on exploration that endogenously discounts the current exploration reward by the past accumulative amount of exploration. Such a recursive regularization restores the optimality of Gaussian exploration. However, contrary to the existing results, the optimal Gaussian policy turns out to be biased in general, due to the interwinding needs for hedging and for exploration. We present an asymptotic analysis of the resulting errors to show how the level of exploration affects the learned policies. Furthermore, we establish a policy improvement theorem and design several RL algorithms to learn Merton's optimal strategies. At last, we carry out both simulation and empirical studies with a stochastic volatility environment to demonstrate the efficiency and robustness of the RL algorithms in comparison to the conventional plug-in method.

q-Learning in Continuous Time

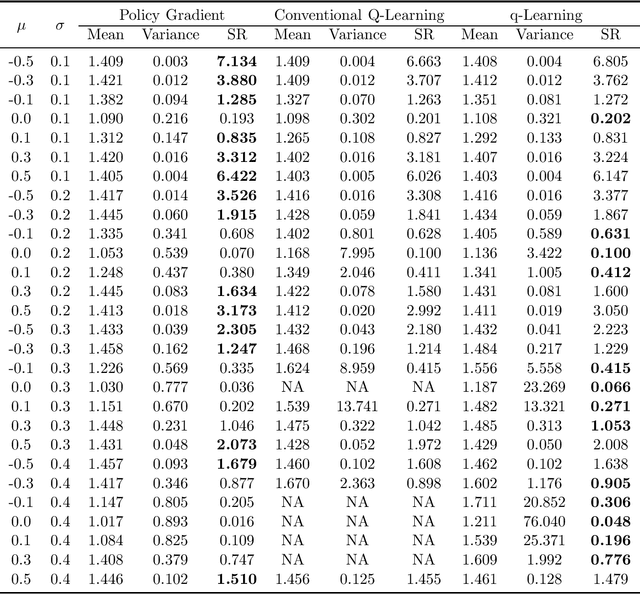
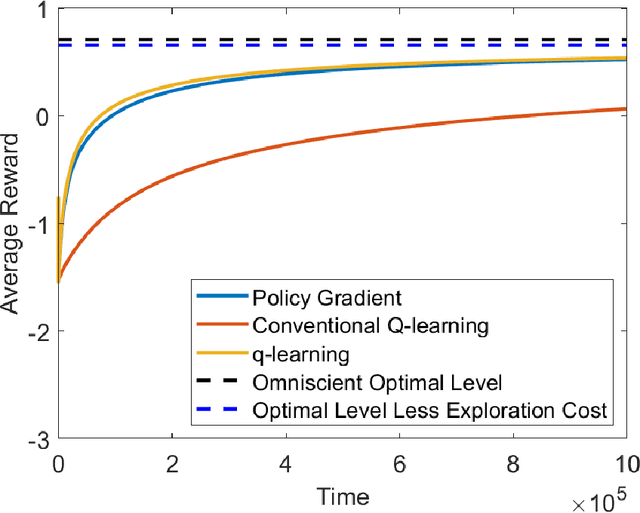
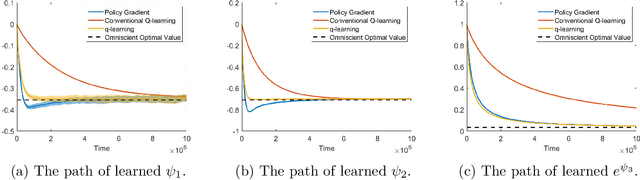
We study the continuous-time counterpart of Q-learning for reinforcement learning (RL) under the entropy-regularized, exploratory diffusion process formulation introduced by Wang et al. (2020) As the conventional (big) Q-function collapses in continuous time, we consider its first-order approximation and coin the term "(little) q-function". This function is related to the instantaneous advantage rate function as well as the Hamiltonian. We develop a "q-learning" theory around the q-function that is independent of time discretization. Given a stochastic policy, we jointly characterize the associated q-function and value function by martingale conditions of certain stochastic processes. We then apply the theory to devise different actor-critic algorithms for solving underlying RL problems, depending on whether or not the density function of the Gibbs measure generated from the q-function can be computed explicitly. One of our algorithms interprets the well-known Q-learning algorithm SARSA, and another recovers a policy gradient (PG) based continuous-time algorithm proposed in Jia and Zhou (2021). Finally, we conduct simulation experiments to compare the performance of our algorithms with those of PG-based algorithms in Jia and Zhou (2021) and time-discretized conventional Q-learning algorithms.

Policy Gradient and Actor-Critic Learning in Continuous Time and Space: Theory and Algorithms

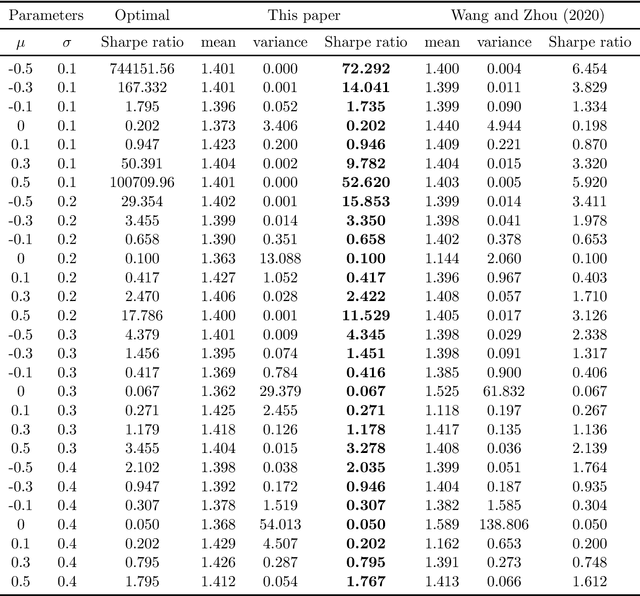
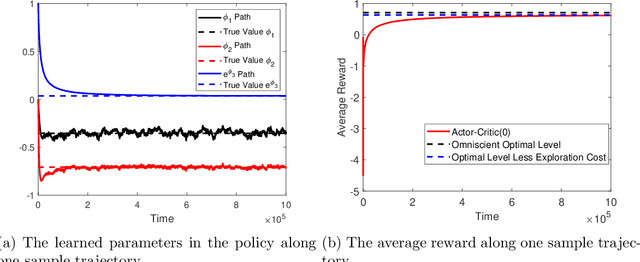
We study policy gradient (PG) for reinforcement learning in continuous time and space under the regularized exploratory formulation developed by Wang et al. (2020). We represent the gradient of the value function with respect to a given parameterized stochastic policy as the expected integration of an auxiliary running reward function that can be evaluated using samples and the current value function. This effectively turns PG into a policy evaluation (PE) problem, enabling us to apply the martingale approach recently developed by Jia and Zhou (2021) for PE to solve our PG problem. Based on this analysis, we propose two types of the actor-critic algorithms for RL, where we learn and update value functions and policies simultaneously and alternatingly. The first type is based directly on the aforementioned representation which involves future trajectories and hence is offline. The second type, designed for online learning, employs the first-order condition of the policy gradient and turns it into martingale orthogonality conditions. These conditions are then incorporated using stochastic approximation when updating policies. Finally, we demonstrate the algorithms by simulations in two concrete examples.

Policy Evaluation and Temporal-Difference Learning in Continuous Time and Space: A Martingale Approach

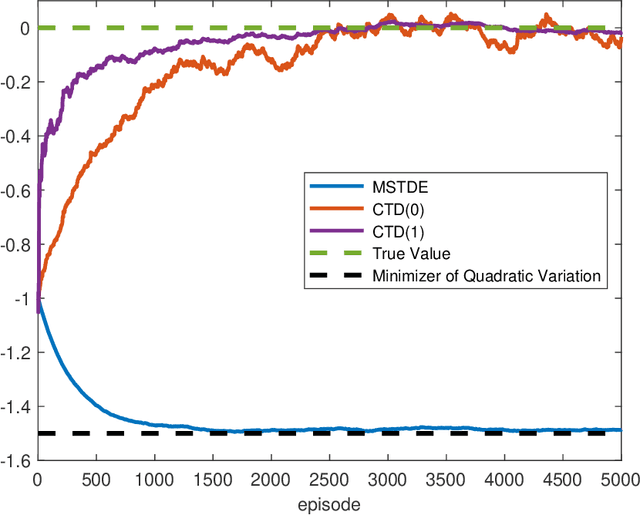
We propose a unified framework to study policy evaluation (PE) and the associated temporal difference (TD) methods for reinforcement learning in continuous time and space. We show that PE is equivalent to maintaining the martingale condition of a process. From this perspective, we find that the mean--square TD error approximates the quadratic variation of the martingale and thus is not a suitable objective for PE. We present two methods to use the martingale characterization for designing PE algorithms. The first one minimizes a "martingale loss function", whose solution is proved to be the best approximation of the true value function in the mean--square sense. This method interprets the classical gradient Monte-Carlo algorithm. The second method is based on a system of equations called the "martingale orthogonality conditions" with "test functions". Solving these equations in different ways recovers various classical TD algorithms, such as TD($\lambda$), LSTD, and GTD. Different choices of test functions determine in what sense the resulting solutions approximate the true value function. Moreover, we prove that any convergent time-discretized algorithm converges to its continuous-time counterpart as the mesh size goes to zero. We demonstrate the theoretical results and corresponding algorithms with numerical experiments and applications.