Mem2Ego: Empowering Vision-Language Models with Global-to-Ego Memory for Long-Horizon Embodied Navigation

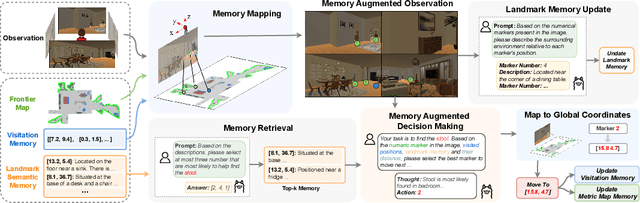
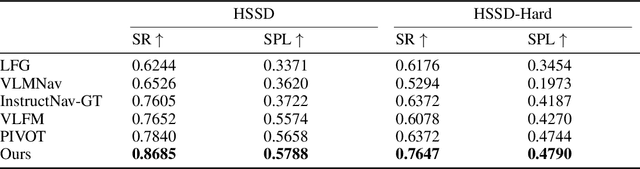
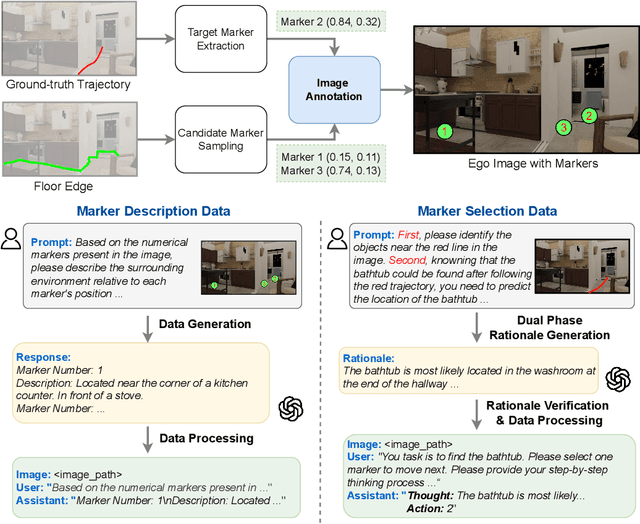
Recent advancements in Large Language Models (LLMs) and Vision-Language Models (VLMs) have made them powerful tools in embodied navigation, enabling agents to leverage commonsense and spatial reasoning for efficient exploration in unfamiliar environments. Existing LLM-based approaches convert global memory, such as semantic or topological maps, into language descriptions to guide navigation. While this improves efficiency and reduces redundant exploration, the loss of geometric information in language-based representations hinders spatial reasoning, especially in intricate environments. To address this, VLM-based approaches directly process ego-centric visual inputs to select optimal directions for exploration. However, relying solely on a first-person perspective makes navigation a partially observed decision-making problem, leading to suboptimal decisions in complex environments. In this paper, we present a novel vision-language model (VLM)-based navigation framework that addresses these challenges by adaptively retrieving task-relevant cues from a global memory module and integrating them with the agent's egocentric observations. By dynamically aligning global contextual information with local perception, our approach enhances spatial reasoning and decision-making in long-horizon tasks. Experimental results demonstrate that the proposed method surpasses previous state-of-the-art approaches in object navigation tasks, providing a more effective and scalable solution for embodied navigation.

Towards Principled, Practical Policy Gradient for Bandits and Tabular MDPs

We consider (stochastic) softmax policy gradient (PG) methods for bandits and tabular Markov decision processes (MDPs). While the PG objective is non-concave, recent research has used the objective's smoothness and gradient domination properties to achieve convergence to an optimal policy. However, these theoretical results require setting the algorithm parameters according to unknown problem-dependent quantities (e.g. the optimal action or the true reward vector in a bandit problem). To address this issue, we borrow ideas from the optimization literature to design practical, principled PG methods in both the exact and stochastic settings. In the exact setting, we employ an Armijo line-search to set the step-size for softmax PG and empirically demonstrate a linear convergence rate. In the stochastic setting, we utilize exponentially decreasing step-sizes, and characterize the convergence rate of the resulting algorithm. We show that the proposed algorithm offers similar theoretical guarantees as the state-of-the art results, but does not require the knowledge of oracle-like quantities. For the multi-armed bandit setting, our techniques result in a theoretically-principled PG algorithm that does not require explicit exploration, the knowledge of the reward gap, the reward distributions, or the noise. Finally, we empirically compare the proposed methods to PG approaches that require oracle knowledge, and demonstrate competitive performance.