Approximation of optimization problems with constraints through kernel Sum-Of-Squares

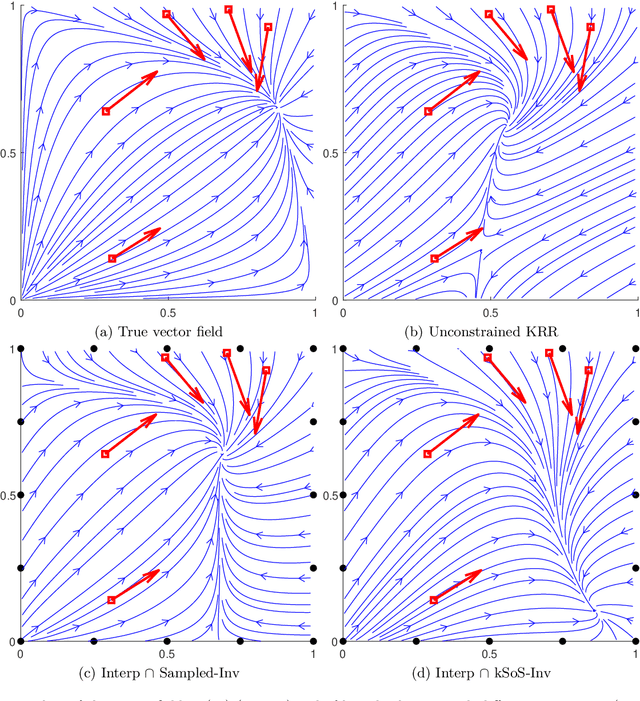
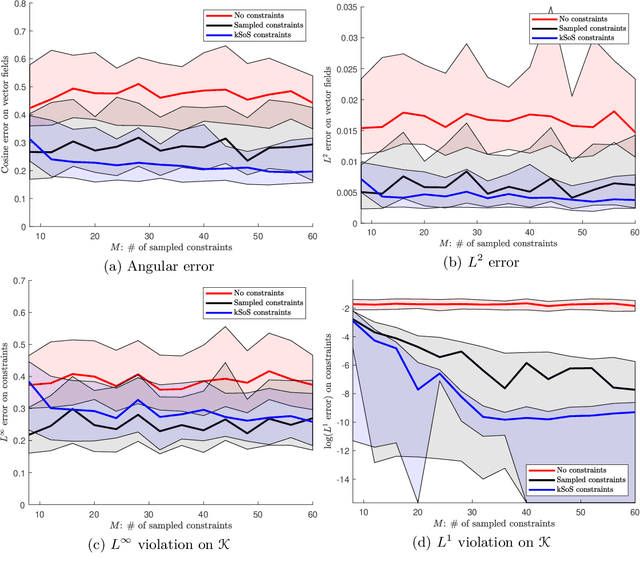
Handling an infinite number of inequality constraints in infinite-dimensional spaces occurs in many fields, from global optimization to optimal transport. These problems have been tackled individually in several previous articles through kernel Sum-Of-Squares (kSoS) approximations. We propose here a unified theorem to prove convergence guarantees for these schemes. Inequalities are turned into equalities to a class of nonnegative kSoS functions. This enables the use of scattering inequalities to mitigate the curse of dimensionality in sampling the constraints, leveraging the assumed smoothness of the functions appearing in the problem. This approach is illustrated in learning vector fields with side information, here the invariance of a set.