Joey Bose
EDGI: Equivariant Diffusion for Planning with Embodied Agents
Mar 22, 2023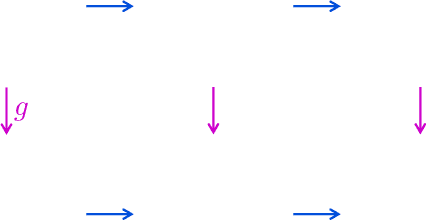
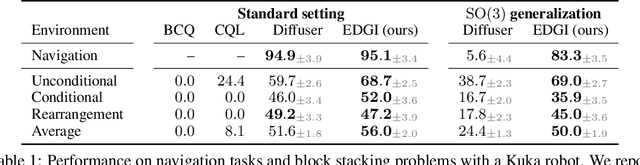
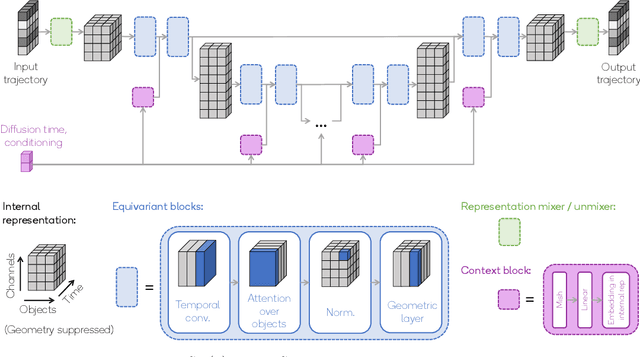
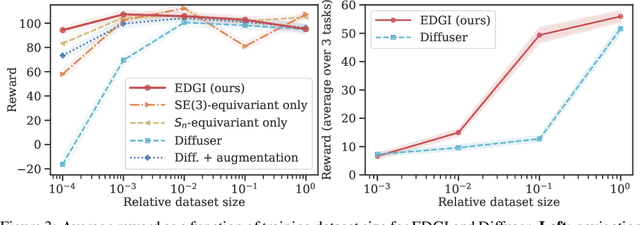
Abstract:Embodied agents operate in a structured world, often solving tasks with spatial, temporal, and permutation symmetries. Most algorithms for planning and model-based reinforcement learning (MBRL) do not take this rich geometric structure into account, leading to sample inefficiency and poor generalization. We introduce the Equivariant Diffuser for Generating Interactions (EDGI), an algorithm for MBRL and planning that is equivariant with respect to the product of the spatial symmetry group $\mathrm{SE(3)}$, the discrete-time translation group $\mathbb{Z}$, and the object permutation group $\mathrm{S}_n$. EDGI follows the Diffuser framework (Janner et al. 2022) in treating both learning a world model and planning in it as a conditional generative modeling problem, training a diffusion model on an offline trajectory dataset. We introduce a new $\mathrm{SE(3)} \times \mathbb{Z} \times \mathrm{S}_n$-equivariant diffusion model that supports multiple representations. We integrate this model in a planning loop, where conditioning and classifier-based guidance allow us to softly break the symmetry for specific tasks as needed. On navigation and object manipulation tasks, EDGI improves sample efficiency and generalization.
Matching Normalizing Flows and Probability Paths on Manifolds
Jul 11, 2022
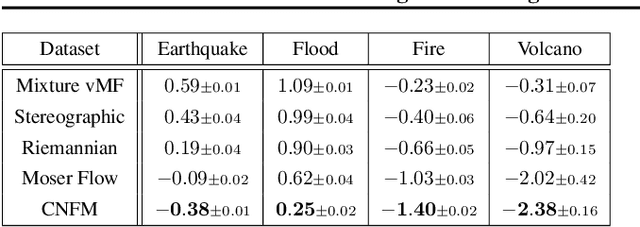
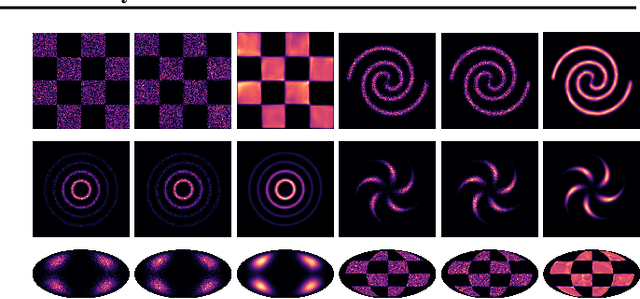
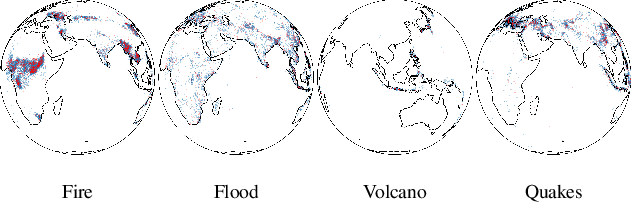
Abstract:Continuous Normalizing Flows (CNFs) are a class of generative models that transform a prior distribution to a model distribution by solving an ordinary differential equation (ODE). We propose to train CNFs on manifolds by minimizing probability path divergence (PPD), a novel family of divergences between the probability density path generated by the CNF and a target probability density path. PPD is formulated using a logarithmic mass conservation formula which is a linear first order partial differential equation relating the log target probabilities and the CNF's defining vector field. PPD has several key benefits over existing methods: it sidesteps the need to solve an ODE per iteration, readily applies to manifold data, scales to high dimensions, and is compatible with a large family of target paths interpolating pure noise and data in finite time. Theoretically, PPD is shown to bound classical probability divergences. Empirically, we show that CNFs learned by minimizing PPD achieve state-of-the-art results in likelihoods and sample quality on existing low-dimensional manifold benchmarks, and is the first example of a generative model to scale to moderately high dimensional manifolds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge