Generalization Properties of Optimal Transport GANs with Latent Distribution Learning
Paper and Code
Jul 29, 2020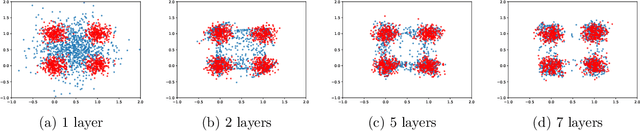
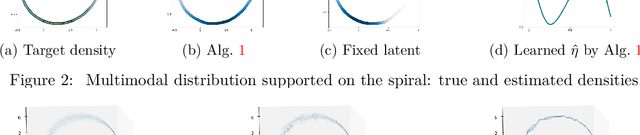
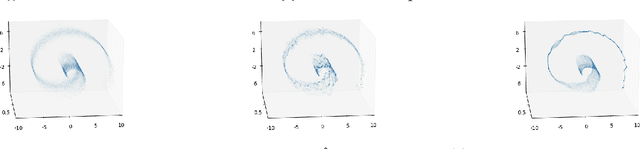
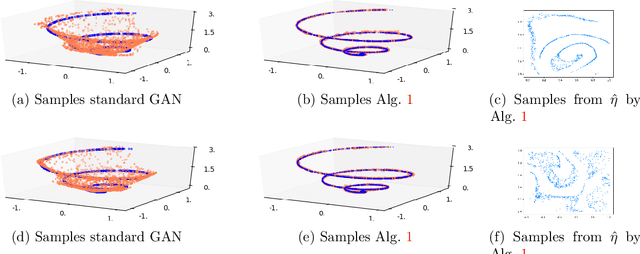
The Generative Adversarial Networks (GAN) framework is a well-established paradigm for probability matching and realistic sample generation. While recent attention has been devoted to studying the theoretical properties of such models, a full theoretical understanding of the main building blocks is still missing. Focusing on generative models with Optimal Transport metrics as discriminators, in this work we study how the interplay between the latent distribution and the complexity of the pushforward map (generator) affects performance, from both statistical and modelling perspectives. Motivated by our analysis, we advocate learning the latent distribution as well as the pushforward map within the GAN paradigm. We prove that this can lead to significant advantages in terms of sample complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge