Exponential Moving Average of Weights in Deep Learning: Dynamics and Benefits

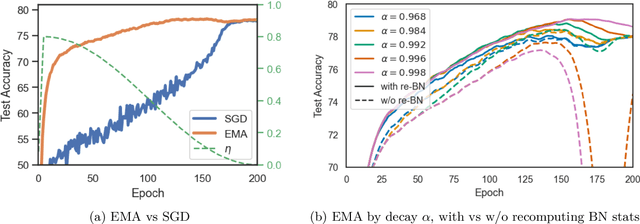
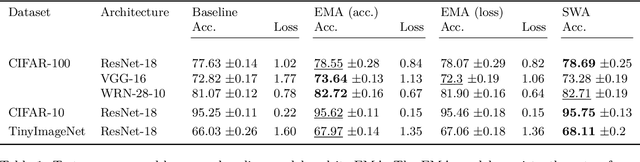
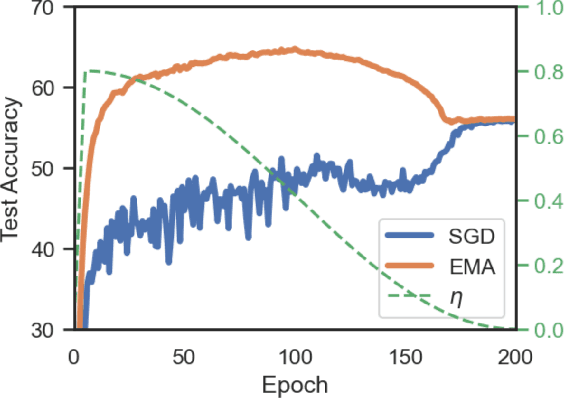
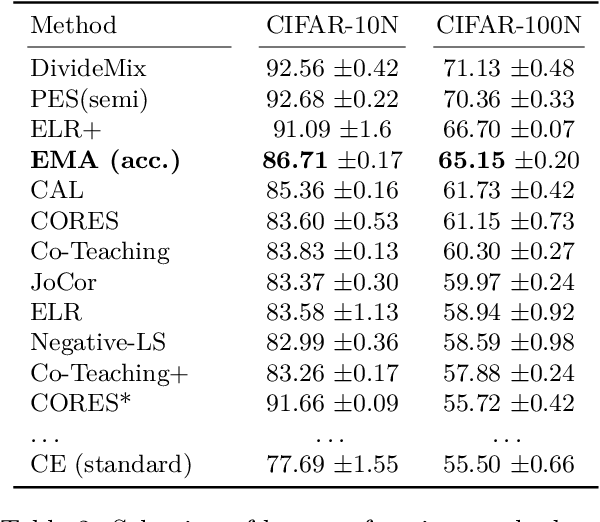
Weight averaging of Stochastic Gradient Descent (SGD) iterates is a popular method for training deep learning models. While it is often used as part of complex training pipelines to improve generalization or serve as a `teacher' model, weight averaging lacks proper evaluation on its own. In this work, we present a systematic study of the Exponential Moving Average (EMA) of weights. We first explore the training dynamics of EMA, give guidelines for hyperparameter tuning, and highlight its good early performance, partly explaining its success as a teacher. We also observe that EMA requires less learning rate decay compared to SGD since averaging naturally reduces noise, introducing a form of implicit regularization. Through extensive experiments, we show that EMA solutions differ from last-iterate solutions. EMA models not only generalize better but also exhibit improved i) robustness to noisy labels, ii) prediction consistency, iii) calibration and iv) transfer learning. Therefore, we suggest that an EMA of weights is a simple yet effective plug-in to improve the performance of deep learning models.

The Last Mile to Supervised Performance: Semi-Supervised Domain Adaptation for Semantic Segmentation

Supervised deep learning requires massive labeled datasets, but obtaining annotations is not always easy or possible, especially for dense tasks like semantic segmentation. To overcome this issue, numerous works explore Unsupervised Domain Adaptation (UDA), which uses a labeled dataset from another domain (source), or Semi-Supervised Learning (SSL), which trains on a partially labeled set. Despite the success of UDA and SSL, reaching supervised performance at a low annotation cost remains a notoriously elusive goal. To address this, we study the promising setting of Semi-Supervised Domain Adaptation (SSDA). We propose a simple SSDA framework that combines consistency regularization, pixel contrastive learning, and self-training to effectively utilize a few target-domain labels. Our method outperforms prior art in the popular GTA-to-Cityscapes benchmark and shows that as little as 50 target labels can suffice to achieve near-supervised performance. Additional results on Synthia-to-Cityscapes, GTA-to-BDD and Synthia-to-BDD further demonstrate the effectiveness and practical utility of the method. Lastly, we find that existing UDA and SSL methods are not well-suited for the SSDA setting and discuss design patterns to adapt them.