The Last Mile to Supervised Performance: Semi-Supervised Domain Adaptation for Semantic Segmentation

Supervised deep learning requires massive labeled datasets, but obtaining annotations is not always easy or possible, especially for dense tasks like semantic segmentation. To overcome this issue, numerous works explore Unsupervised Domain Adaptation (UDA), which uses a labeled dataset from another domain (source), or Semi-Supervised Learning (SSL), which trains on a partially labeled set. Despite the success of UDA and SSL, reaching supervised performance at a low annotation cost remains a notoriously elusive goal. To address this, we study the promising setting of Semi-Supervised Domain Adaptation (SSDA). We propose a simple SSDA framework that combines consistency regularization, pixel contrastive learning, and self-training to effectively utilize a few target-domain labels. Our method outperforms prior art in the popular GTA-to-Cityscapes benchmark and shows that as little as 50 target labels can suffice to achieve near-supervised performance. Additional results on Synthia-to-Cityscapes, GTA-to-BDD and Synthia-to-BDD further demonstrate the effectiveness and practical utility of the method. Lastly, we find that existing UDA and SSL methods are not well-suited for the SSDA setting and discuss design patterns to adapt them.

Learning to Remove Cuts in Integer Linear Programming

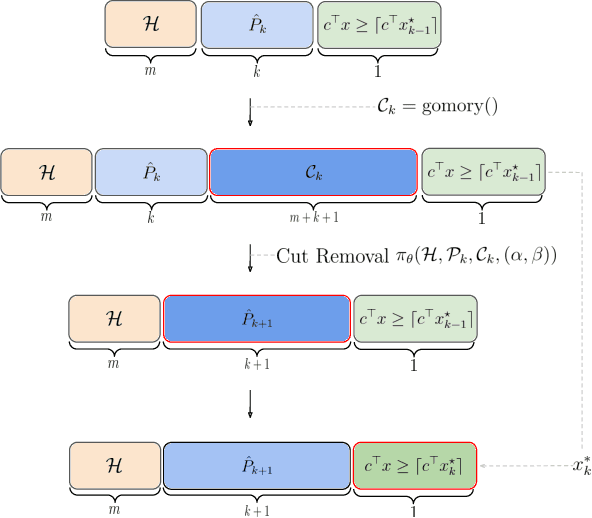
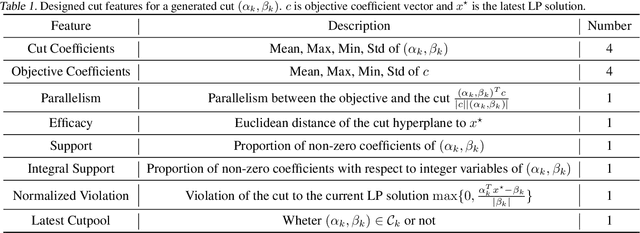
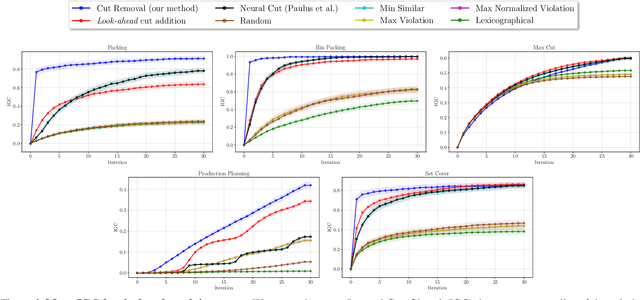
Cutting plane methods are a fundamental approach for solving integer linear programs (ILPs). In each iteration of such methods, additional linear constraints (cuts) are introduced to the constraint set with the aim of excluding the previous fractional optimal solution while not affecting the optimal integer solution. In this work, we explore a novel approach within cutting plane methods: instead of only adding new cuts, we also consider the removal of previous cuts introduced at any of the preceding iterations of the method under a learnable parametric criteria. We demonstrate that in fundamental combinatorial optimization settings such cut removal policies can lead to significant improvements over both human-based and machine learning-guided cut addition policies even when implemented with simple models.

Going beyond compositional generalization, DDPMs can produce zero-shot interpolation

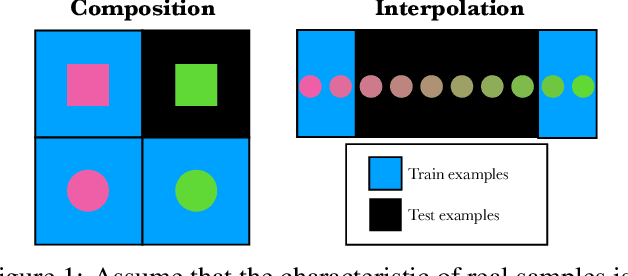
Denoising Diffusion Probabilistic Models (DDPMs) exhibit remarkable capabilities in image generation, with studies suggesting that they can generalize by composing latent factors learned from the training data. In this work, we go further and study DDPMs trained on strictly separate subsets of the data distribution with large gaps on the support of the latent factors. We show that such a model can effectively generate images in the unexplored, intermediate regions of the distribution. For instance, when trained on clearly smiling and non-smiling faces, we demonstrate a sampling procedure which can generate slightly smiling faces without reference images (zero-shot interpolation). We replicate these findings for other attributes as well as other datasets. $\href{https://github.com/jdeschena/ddpm-zero-shot-interpolation}{\text{Our code is available on GitHub.}}$

Federated Learning under Covariate Shifts with Generalization Guarantees

This paper addresses intra-client and inter-client covariate shifts in federated learning (FL) with a focus on the overall generalization performance. To handle covariate shifts, we formulate a new global model training paradigm and propose Federated Importance-Weighted Empirical Risk Minimization (FTW-ERM) along with improving density ratio matching methods without requiring perfect knowledge of the supremum over true ratios. We also propose the communication-efficient variant FITW-ERM with the same level of privacy guarantees as those of classical ERM in FL. We theoretically show that FTW-ERM achieves smaller generalization error than classical ERM under certain settings. Experimental results demonstrate the superiority of FTW-ERM over existing FL baselines in challenging imbalanced federated settings in terms of data distribution shifts across clients.

The Spectral Bias of Polynomial Neural Networks

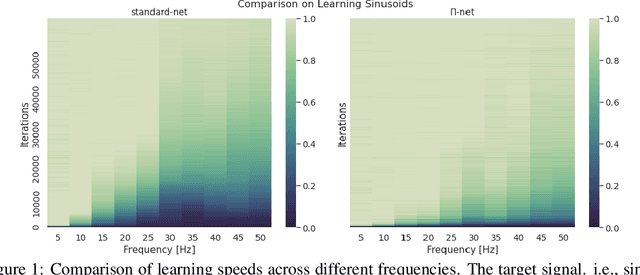
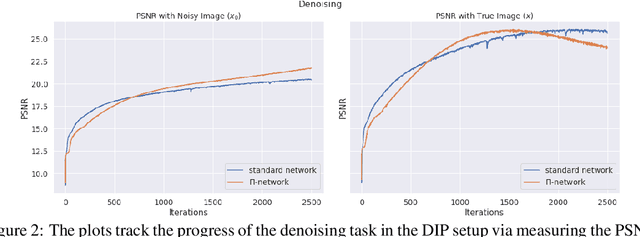
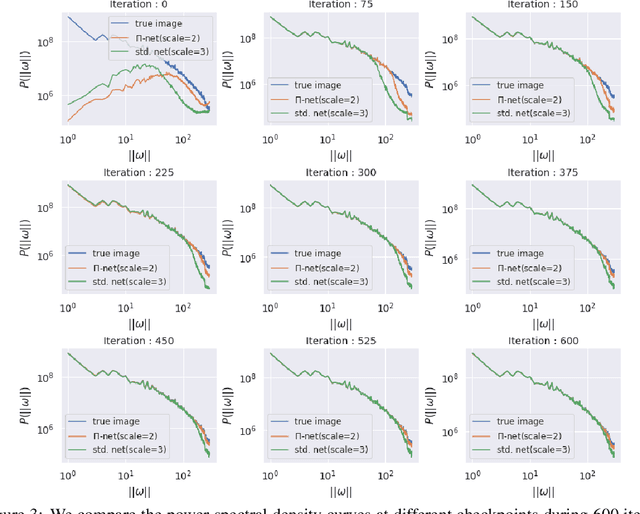
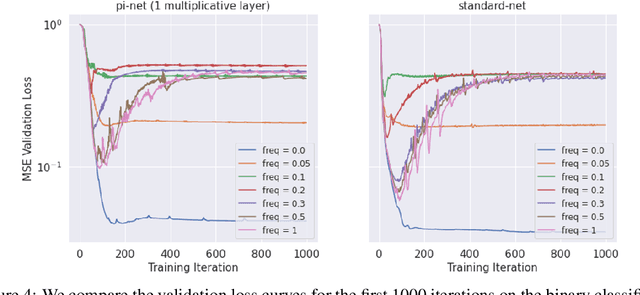
Polynomial neural networks (PNNs) have been recently shown to be particularly effective at image generation and face recognition, where high-frequency information is critical. Previous studies have revealed that neural networks demonstrate a $\textit{spectral bias}$ towards low-frequency functions, which yields faster learning of low-frequency components during training. Inspired by such studies, we conduct a spectral analysis of the Neural Tangent Kernel (NTK) of PNNs. We find that the $\Pi$-Net family, i.e., a recently proposed parametrization of PNNs, speeds up the learning of the higher frequencies. We verify the theoretical bias through extensive experiments. We expect our analysis to provide novel insights into designing architectures and learning frameworks by incorporating multiplicative interactions via polynomials.

Poly-NL: Linear Complexity Non-local Layers with Polynomials

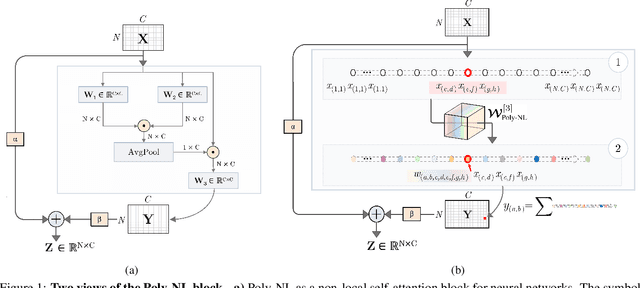
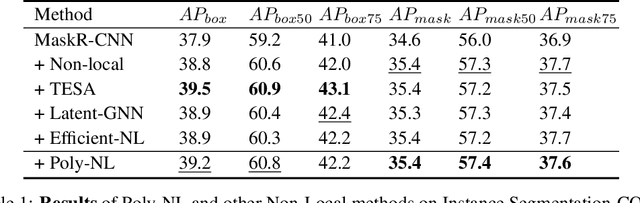
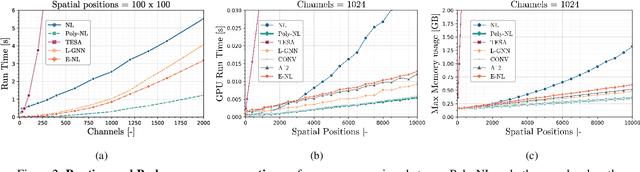
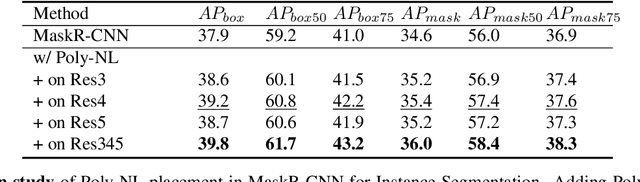
Spatial self-attention layers, in the form of Non-Local blocks, introduce long-range dependencies in Convolutional Neural Networks by computing pairwise similarities among all possible positions. Such pairwise functions underpin the effectiveness of non-local layers, but also determine a complexity that scales quadratically with respect to the input size both in space and time. This is a severely limiting factor that practically hinders the applicability of non-local blocks to even moderately sized inputs. Previous works focused on reducing the complexity by modifying the underlying matrix operations, however in this work we aim to retain full expressiveness of non-local layers while keeping complexity linear. We overcome the efficiency limitation of non-local blocks by framing them as special cases of 3rd order polynomial functions. This fact enables us to formulate novel fast Non-Local blocks, capable of reducing the complexity from quadratic to linear with no loss in performance, by replacing any direct computation of pairwise similarities with element-wise multiplications. The proposed method, which we dub as "Poly-NL", is competitive with state-of-the-art performance across image recognition, instance segmentation, and face detection tasks, while having considerably less computational overhead.

Multilinear Latent Conditioning for Generating Unseen Attribute Combinations

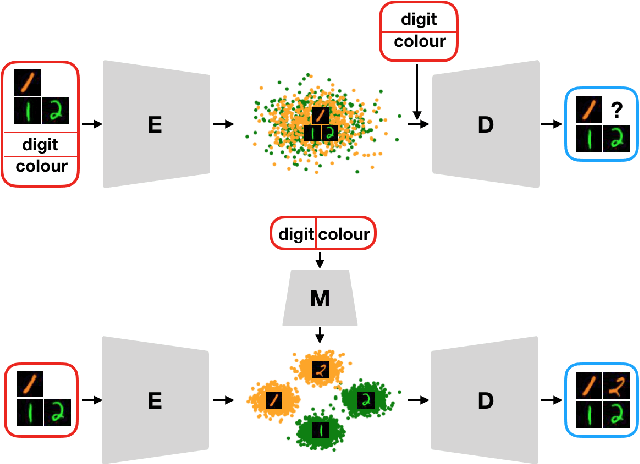
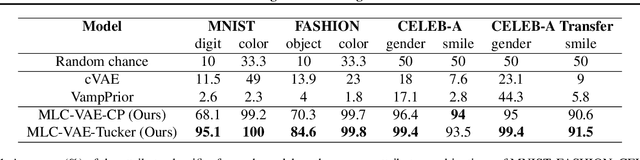
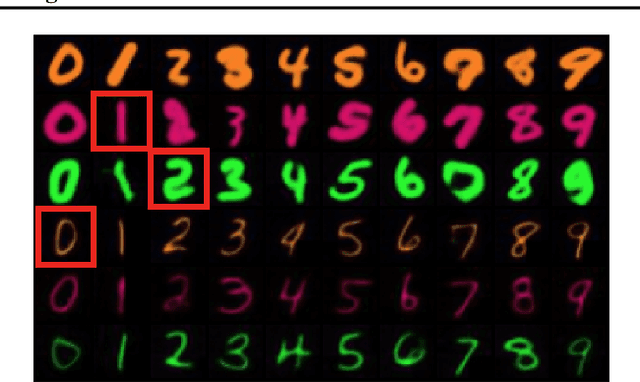
Deep generative models rely on their inductive bias to facilitate generalization, especially for problems with high dimensional data, like images. However, empirical studies have shown that variational autoencoders (VAE) and generative adversarial networks (GAN) lack the generalization ability that occurs naturally in human perception. For example, humans can visualize a woman smiling after only seeing a smiling man. On the contrary, the standard conditional VAE (cVAE) is unable to generate unseen attribute combinations. To this end, we extend cVAE by introducing a multilinear latent conditioning framework that captures the multiplicative interactions between the attributes. We implement two variants of our model and demonstrate their efficacy on MNIST, Fashion-MNIST and CelebA. Altogether, we design a novel conditioning framework that can be used with any architecture to synthesize unseen attribute combinations.

Deep Polynomial Neural Networks

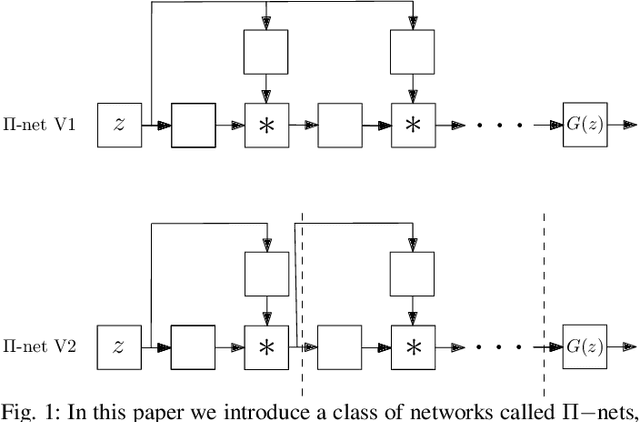
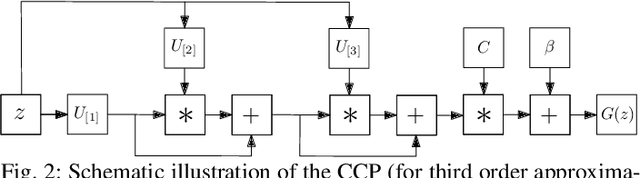
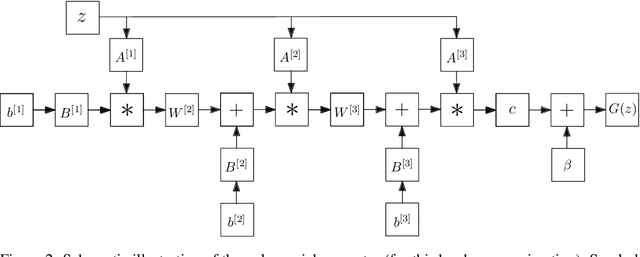
Deep Convolutional Neural Networks (DCNNs) are currently the method of choice both for generative, as well as for discriminative learning in computer vision and machine learning. The success of DCNNs can be attributed to the careful selection of their building blocks (e.g., residual blocks, rectifiers, sophisticated normalization schemes, to mention but a few). In this paper, we propose $\Pi$-Nets, a new class of DCNNs. $\Pi$-Nets are polynomial neural networks, i.e., the output is a high-order polynomial of the input. The unknown parameters, which are naturally represented by high-order tensors, are estimated through a collective tensor factorization with factors sharing. We introduce three tensor decompositions that significantly reduce the number of parameters and show how they can be efficiently implemented by hierarchical neural networks. We empirically demonstrate that $\Pi$-Nets are very expressive and they even produce good results without the use of non-linear activation functions in a large battery of tasks and signals, i.e., images, graphs, and audio. When used in conjunction with activation functions, $\Pi$-Nets produce state-of-the-art results in three challenging tasks, i.e. image generation, face verification and 3D mesh representation learning.

PolyGAN: High-Order Polynomial Generators

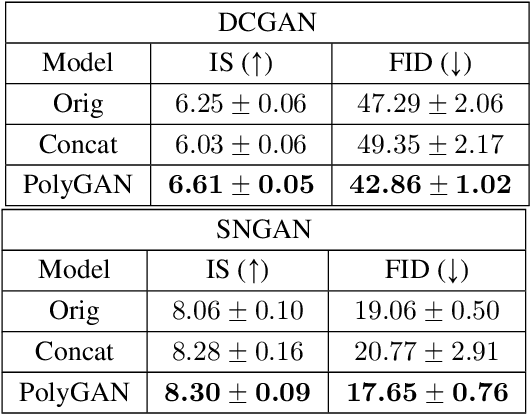
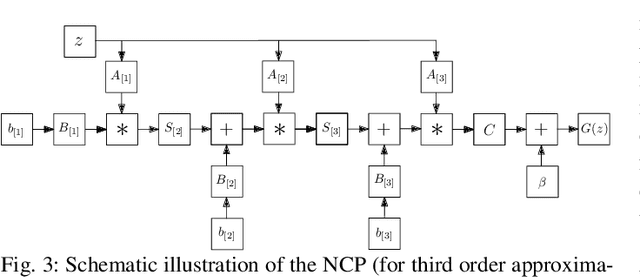
Generative Adversarial Networks (GANs) have become the gold standard when it comes to learning generative models that can describe intricate, high-dimensional distributions. Since their advent, numerous variations of GANs have been introduced in the literature, primarily focusing on utilization of novel loss functions, optimization/regularization strategies and architectures. In this work, we take an orthogonal approach to the above and turn our attention to the generator. We propose to model the data generator by means of a high-order polynomial using tensorial factors. We design a hierarchical decomposition of the polynomial and demonstrate how it can be efficiently implemented by a neural network. We show, for the first time, that by using our decomposition a GAN generator can approximate the data distribution by only using linear/convolution blocks without using any activation functions. Finally, we highlight that PolyGAN can be easily adapted and used along-side all major GAN architectures. In an extensive series of quantitative and qualitative experiments, PolyGAN improves upon the state-of-the-art by a significant margin.