Scale Equivariant Graph Metanetworks

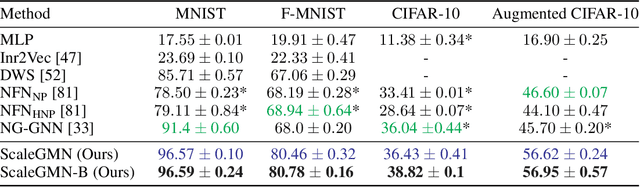
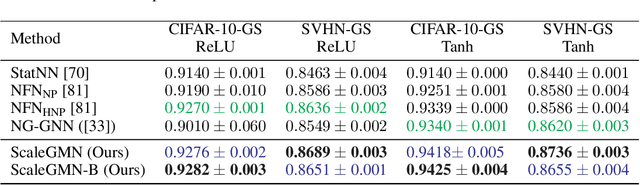
This paper pertains to an emerging machine learning paradigm: learning higher-order functions, i.e. functions whose inputs are functions themselves, $\textit{particularly when these inputs are Neural Networks (NNs)}$. With the growing interest in architectures that process NNs, a recurring design principle has permeated the field: adhering to the permutation symmetries arising from the connectionist structure of NNs. $\textit{However, are these the sole symmetries present in NN parameterizations}$? Zooming into most practical activation functions (e.g. sine, ReLU, tanh) answers this question negatively and gives rise to intriguing new symmetries, which we collectively refer to as $\textit{scaling symmetries}$, that is, non-zero scalar multiplications and divisions of weights and biases. In this work, we propose $\textit{Scale Equivariant Graph MetaNetworks - ScaleGMNs}$, a framework that adapts the Graph Metanetwork (message-passing) paradigm by incorporating scaling symmetries and thus rendering neuron and edge representations equivariant to valid scalings. We introduce novel building blocks, of independent technical interest, that allow for equivariance or invariance with respect to individual scalar multipliers or their product and use them in all components of ScaleGMN. Furthermore, we prove that, under certain expressivity conditions, ScaleGMN can simulate the forward and backward pass of any input feedforward neural network. Experimental results demonstrate that our method advances the state-of-the-art performance for several datasets and activation functions, highlighting the power of scaling symmetries as an inductive bias for NN processing.

Bridging Mini-Batch and Asymptotic Analysis in Contrastive Learning: From InfoNCE to Kernel-Based Losses

What do different contrastive learning (CL) losses actually optimize for? Although multiple CL methods have demonstrated remarkable representation learning capabilities, the differences in their inner workings remain largely opaque. In this work, we analyse several CL families and prove that, under certain conditions, they admit the same minimisers when optimizing either their batch-level objectives or their expectations asymptotically. In both cases, an intimate connection with the hyperspherical energy minimisation (HEM) problem resurfaces. Drawing inspiration from this, we introduce a novel CL objective, coined Decoupled Hyperspherical Energy Loss (DHEL). DHEL simplifies the problem by decoupling the target hyperspherical energy from the alignment of positive examples while preserving the same theoretical guarantees. Going one step further, we show the same results hold for another relevant CL family, namely kernel contrastive learning (KCL), with the additional advantage of the expected loss being independent of batch size, thus identifying the minimisers in the non-asymptotic regime. Empirical results demonstrate improved downstream performance and robustness across combinations of different batch sizes and hyperparameters and reduced dimensionality collapse, on several computer vision datasets.

Revisiting Point Cloud Simplification: A Learnable Feature Preserving Approach

The recent advances in 3D sensing technology have made possible the capture of point clouds in significantly high resolution. However, increased detail usually comes at the expense of high storage, as well as computational costs in terms of processing and visualization operations. Mesh and Point Cloud simplification methods aim to reduce the complexity of 3D models while retaining visual quality and relevant salient features. Traditional simplification techniques usually rely on solving a time-consuming optimization problem, hence they are impractical for large-scale datasets. In an attempt to alleviate this computational burden, we propose a fast point cloud simplification method by learning to sample salient points. The proposed method relies on a graph neural network architecture trained to select an arbitrary, user-defined, number of points from the input space and to re-arrange their positions so as to minimize the visual perception error. The approach is extensively evaluated on various datasets using several perceptual metrics. Importantly, our method is able to generalize to out-of-distribution shapes, hence demonstrating zero-shot capabilities.

Partition and Code: learning how to compress graphs

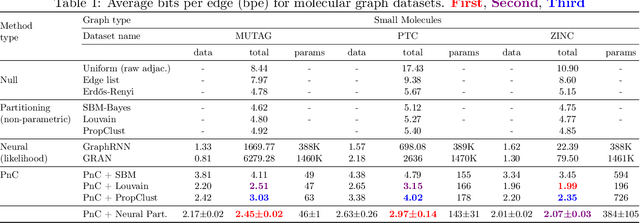
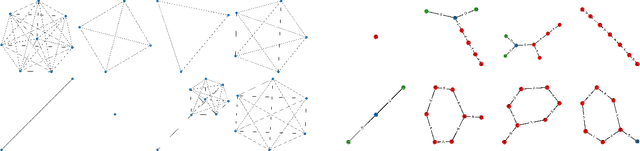
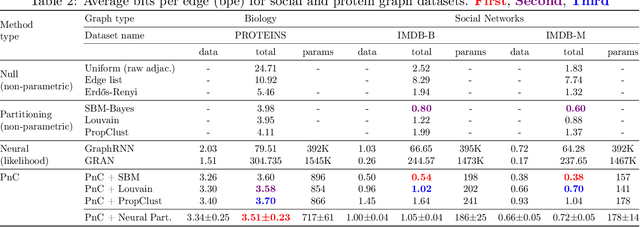
Can we use machine learning to compress graph data? The absence of ordering in graphs poses a significant challenge to conventional compression algorithms, limiting their attainable gains as well as their ability to discover relevant patterns. On the other hand, most graph compression approaches rely on domain-dependent handcrafted representations and cannot adapt to different underlying graph distributions. This work aims to establish the necessary principles a lossless graph compression method should follow to approach the entropy storage lower bound. Instead of making rigid assumptions about the graph distribution, we formulate the compressor as a probabilistic model that can be learned from data and generalise to unseen instances. Our "Partition and Code" framework entails three steps: first, a partitioning algorithm decomposes the graph into elementary structures, then these are mapped to the elements of a small dictionary on which we learn a probability distribution, and finally, an entropy encoder translates the representation into bits. All three steps are parametric and can be trained with gradient descent. We theoretically compare the compression quality of several graph encodings and prove, under mild conditions, a total ordering of their expected description lengths. Moreover, we show that, under the same conditions, PnC achieves compression gains w.r.t. the baselines that grow either linearly or quadratically with the number of vertices. Our algorithms are quantitatively evaluated on diverse real-world networks obtaining significant performance improvements with respect to different families of non-parametric and parametric graph compressors.

3D Facial Matching by Spiral Convolutional Metric Learning and a Biometric Fusion-Net of Demographic Properties

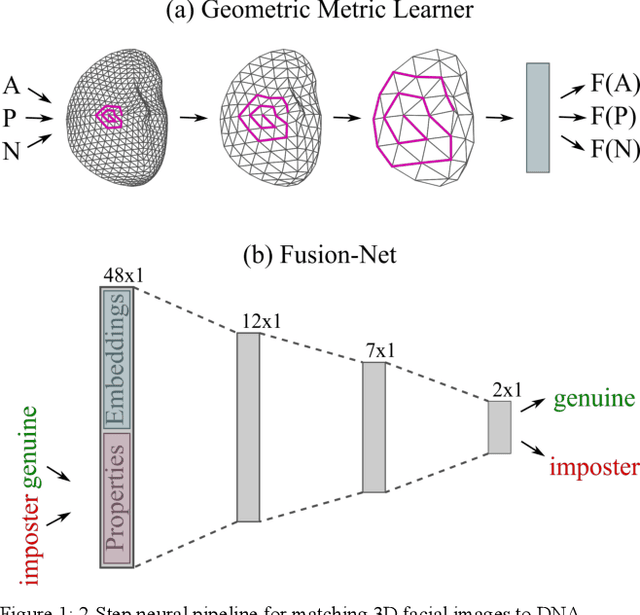
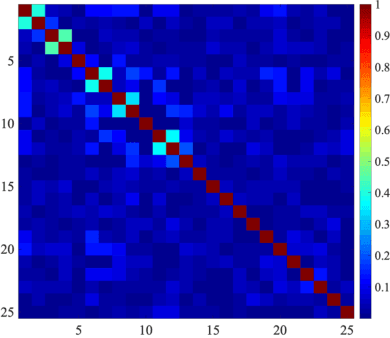
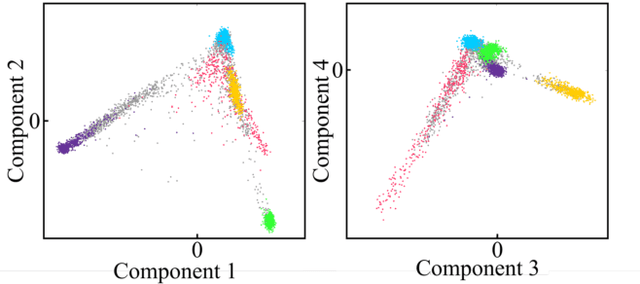
Face recognition is a widely accepted biometric verification tool, as the face contains a lot of information about the identity of a person. In this study, a 2-step neural-based pipeline is presented for matching 3D facial shape to multiple DNA-related properties (sex, age, BMI and genomic background). The first step consists of a triplet loss-based metric learner that compresses facial shape into a lower dimensional embedding while preserving information about the property of interest. Most studies in the field of metric learning have only focused on Euclidean data. In this work, geometric deep learning is employed to learn directly from 3D facial meshes. To this end, spiral convolutions are used along with a novel mesh-sampling scheme that retains uniformly sampled 3D points at different levels of resolution. The second step is a multi-biometric fusion by a fully connected neural network. The network takes an ensemble of embeddings and property labels as input and returns genuine and imposter scores. Since embeddings are accepted as an input, there is no need to train classifiers for the different properties and available data can be used more efficiently. Results obtained by a 10-fold cross-validation for biometric verification show that combining multiple properties leads to stronger biometric systems. Furthermore, the proposed neural-based pipeline outperforms a linear baseline, which consists of principal component analysis, followed by classification with linear support vector machines and a Naive Bayes-based score-fuser.

Learning to Generate Customized Dynamic 3D Facial Expressions

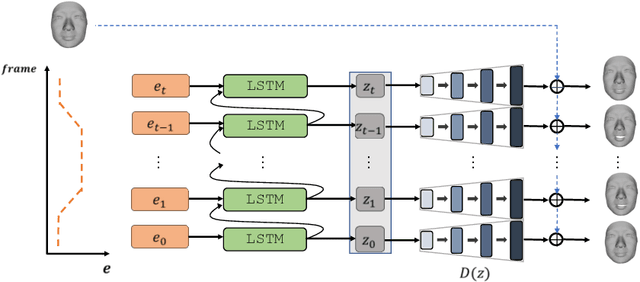
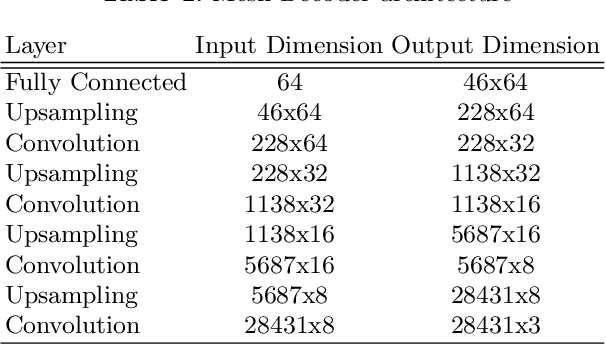
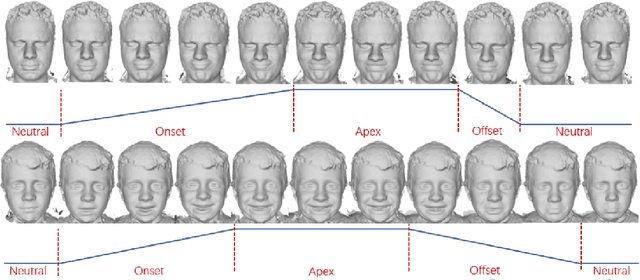
Recent advances in deep learning have significantly pushed the state-of-the-art in photorealistic video animation given a single image. In this paper, we extrapolate those advances to the 3D domain, by studying 3D image-to-video translation with a particular focus on 4D facial expressions. Although 3D facial generative models have been widely explored during the past years, 4D animation remains relatively unexplored. To this end, in this study we employ a deep mesh encoder-decoder like architecture to synthesize realistic high resolution facial expressions by using a single neutral frame along with an expression identification. In addition, processing 3D meshes remains a non-trivial task compared to data that live on grid-like structures, such as images. Given the recent progress in mesh processing with graph convolutions, we make use of a recently introduced learnable operator which acts directly on the mesh structure by taking advantage of local vertex orderings. In order to generalize to 4D facial expressions across subjects, we trained our model using a high resolution dataset with 4D scans of six facial expressions from 180 subjects. Experimental results demonstrate that our approach preserves the subject's identity information even for unseen subjects and generates high quality expressions. To the best of our knowledge, this is the first study tackling the problem of 4D facial expression synthesis.

Deep Polynomial Neural Networks

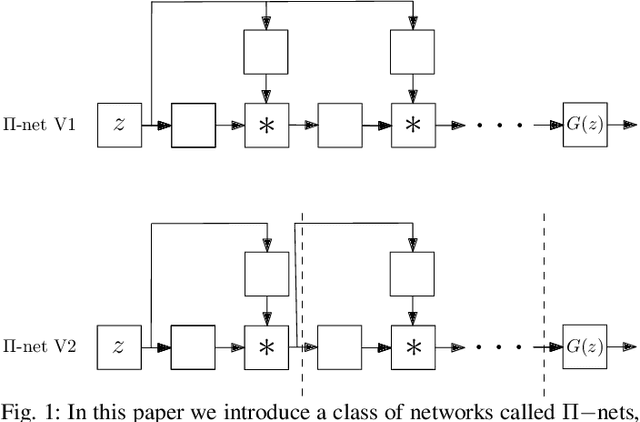
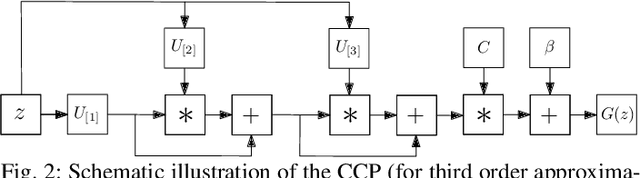
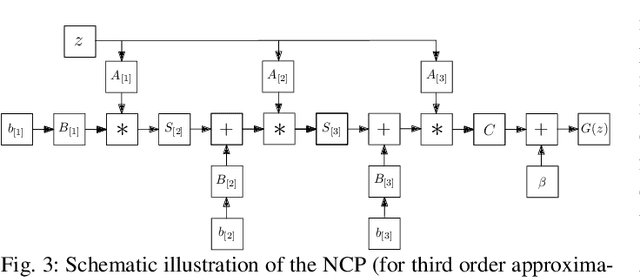
Deep Convolutional Neural Networks (DCNNs) are currently the method of choice both for generative, as well as for discriminative learning in computer vision and machine learning. The success of DCNNs can be attributed to the careful selection of their building blocks (e.g., residual blocks, rectifiers, sophisticated normalization schemes, to mention but a few). In this paper, we propose $\Pi$-Nets, a new class of DCNNs. $\Pi$-Nets are polynomial neural networks, i.e., the output is a high-order polynomial of the input. The unknown parameters, which are naturally represented by high-order tensors, are estimated through a collective tensor factorization with factors sharing. We introduce three tensor decompositions that significantly reduce the number of parameters and show how they can be efficiently implemented by hierarchical neural networks. We empirically demonstrate that $\Pi$-Nets are very expressive and they even produce good results without the use of non-linear activation functions in a large battery of tasks and signals, i.e., images, graphs, and audio. When used in conjunction with activation functions, $\Pi$-Nets produce state-of-the-art results in three challenging tasks, i.e. image generation, face verification and 3D mesh representation learning.

Improving Graph Neural Network Expressivity via Subgraph Isomorphism Counting

While Graph Neural Networks (GNNs) have achieved remarkable results in a variety of applications, recent studies exposed important shortcomings in their ability to capture the structure of the underlying graph. It has been shown that the expressive power of standard GNNs is bounded by the Weisfeiler-Lehman (WL) graph isomorphism test, from which they inherit proven limitations such as the inability to detect and count graph substructures. On the other hand, there is significant empirical evidence, e.g. in network science and bioinformatics, that substructures are often informative for downstream tasks, suggesting that it is desirable to design GNNs capable of leveraging this important source of information. To this end, we propose a novel topologically-aware message passing scheme based on subgraph isomorphism counting. We show that our architecture allows incorporating domain-specific inductive biases and that it is strictly more expressive than the WL test. Importantly, in contrast to recent works on the expressivity of GNNs, we do not attempt to adhere to the WL hierarchy; this allows us to retain multiple attractive properties of standard GNNs such as locality and linear complexity, while being able to disambiguate even hard instances of graph isomorphism. We extensively evaluate our method on graph classification and regression tasks and show state-of-the-art results on multiple datasets including molecular graphs and social networks.

$Π-$nets: Deep Polynomial Neural Networks

Deep Convolutional Neural Networks (DCNNs) is currently the method of choice both for generative, as well as for discriminative learning in computer vision and machine learning. The success of DCNNs can be attributed to the careful selection of their building blocks (e.g., residual blocks, rectifiers, sophisticated normalization schemes, to mention but a few). In this paper, we propose $\Pi$-Nets, a new class of DCNNs. $\Pi$-Nets are polynomial neural networks, i.e., the output is a high-order polynomial of the input. $\Pi$-Nets can be implemented using special kind of skip connections and their parameters can be represented via high-order tensors. We empirically demonstrate that $\Pi$-Nets have better representation power than standard DCNNs and they even produce good results without the use of non-linear activation functions in a large battery of tasks and signals, i.e., images, graphs, and audio. When used in conjunction with activation functions, $\Pi$-Nets produce state-of-the-art results in challenging tasks, such as image generation. Lastly, our framework elucidates why recent generative models, such as StyleGAN, improve upon their predecessors, e.g., ProGAN.

Automated Real-time Anomaly Detection in Human Trajectories using Sequence to Sequence Networks

Detection of anomalous trajectories is an important problem with potential applications to various domains, such as video surveillance, risk assessment, vessel monitoring and high-energy physics. Modeling the distribution of trajectories with statistical approaches has been a challenging task due to the fact that such time series are usually non stationary and highly dimensional. However, modern machine learning techniques provide robust approaches for data-driven modeling and critical information extraction. In this paper, we propose a Sequence to Sequence architecture for real-time detection of anomalies in human trajectories, in the context of risk-based security. Our detection scheme is tested on a synthetic dataset of diverse and realistic trajectories generated by the ISL iCrowd simulator. The experimental results indicate that our scheme accurately detects motion patterns that deviate from normal behaviors and is promising for future real-world applications.