Scale Equivariant Graph Metanetworks

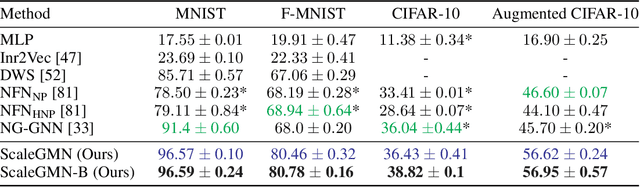
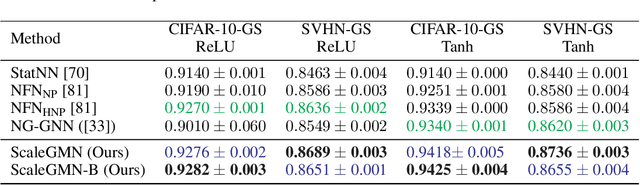
This paper pertains to an emerging machine learning paradigm: learning higher-order functions, i.e. functions whose inputs are functions themselves, $\textit{particularly when these inputs are Neural Networks (NNs)}$. With the growing interest in architectures that process NNs, a recurring design principle has permeated the field: adhering to the permutation symmetries arising from the connectionist structure of NNs. $\textit{However, are these the sole symmetries present in NN parameterizations}$? Zooming into most practical activation functions (e.g. sine, ReLU, tanh) answers this question negatively and gives rise to intriguing new symmetries, which we collectively refer to as $\textit{scaling symmetries}$, that is, non-zero scalar multiplications and divisions of weights and biases. In this work, we propose $\textit{Scale Equivariant Graph MetaNetworks - ScaleGMNs}$, a framework that adapts the Graph Metanetwork (message-passing) paradigm by incorporating scaling symmetries and thus rendering neuron and edge representations equivariant to valid scalings. We introduce novel building blocks, of independent technical interest, that allow for equivariance or invariance with respect to individual scalar multipliers or their product and use them in all components of ScaleGMN. Furthermore, we prove that, under certain expressivity conditions, ScaleGMN can simulate the forward and backward pass of any input feedforward neural network. Experimental results demonstrate that our method advances the state-of-the-art performance for several datasets and activation functions, highlighting the power of scaling symmetries as an inductive bias for NN processing.