Efficient Continual Finite-Sum Minimization

Given a sequence of functions $f_1,\ldots,f_n$ with $f_i:\mathcal{D}\mapsto \mathbb{R}$, finite-sum minimization seeks a point ${x}^\star \in \mathcal{D}$ minimizing $\sum_{j=1}^n f_j(x)/n$. In this work, we propose a key twist into the finite-sum minimization, dubbed as continual finite-sum minimization, that asks for a sequence of points ${x}_1^\star,\ldots,{x}_n^\star \in \mathcal{D}$ such that each ${x}^\star_i \in \mathcal{D}$ minimizes the prefix-sum $\sum_{j=1}^if_j(x)/i$. Assuming that each prefix-sum is strongly convex, we develop a first-order continual stochastic variance reduction gradient method ($\mathrm{CSVRG}$) producing an $\epsilon$-optimal sequence with $\mathcal{\tilde{O}}(n/\epsilon^{1/3} + 1/\sqrt{\epsilon})$ overall first-order oracles (FO). An FO corresponds to the computation of a single gradient $\nabla f_j(x)$ at a given $x \in \mathcal{D}$ for some $j \in [n]$. Our approach significantly improves upon the $\mathcal{O}(n/\epsilon)$ FOs that $\mathrm{StochasticGradientDescent}$ requires and the $\mathcal{O}(n^2 \log (1/\epsilon))$ FOs that state-of-the-art variance reduction methods such as $\mathrm{Katyusha}$ require. We also prove that there is no natural first-order method with $\mathcal{O}\left(n/\epsilon^\alpha\right)$ gradient complexity for $\alpha < 1/4$, establishing that the first-order complexity of our method is nearly tight.

Adaptive Stochastic Variance Reduction for Non-convex Finite-Sum Minimization

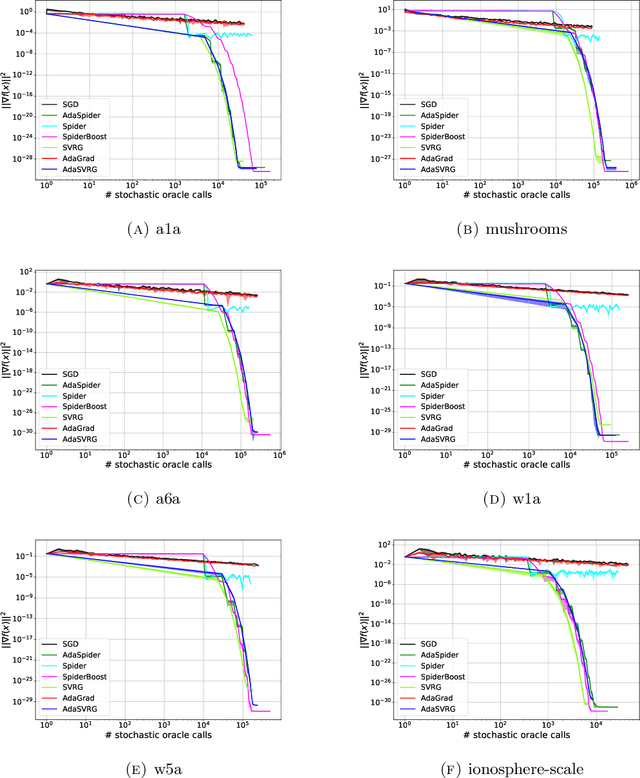
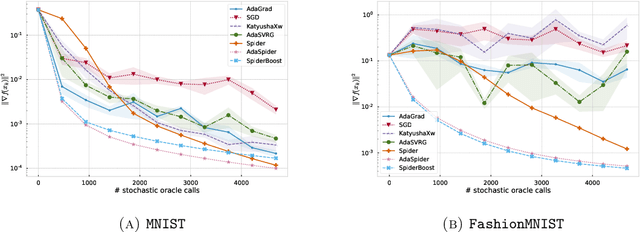
We propose an adaptive variance-reduction method, called AdaSpider, for minimization of $L$-smooth, non-convex functions with a finite-sum structure. In essence, AdaSpider combines an AdaGrad-inspired [Duchi et al., 2011, McMahan & Streeter, 2010], but a fairly distinct, adaptive step-size schedule with the recursive stochastic path integrated estimator proposed in [Fang et al., 2018]. To our knowledge, Adaspider is the first parameter-free non-convex variance-reduction method in the sense that it does not require the knowledge of problem-dependent parameters, such as smoothness constant $L$, target accuracy $\epsilon$ or any bound on gradient norms. In doing so, we are able to compute an $\epsilon$-stationary point with $\tilde{O}\left(n + \sqrt{n}/\epsilon^2\right)$ oracle-calls, which matches the respective lower bound up to logarithmic factors.

The Spectral Bias of Polynomial Neural Networks

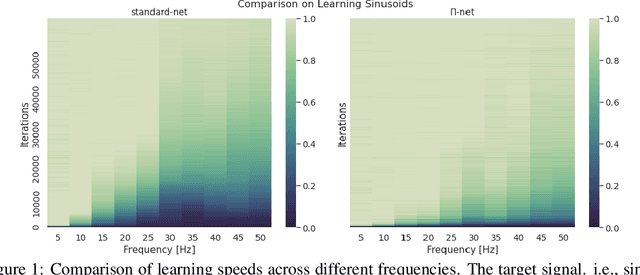
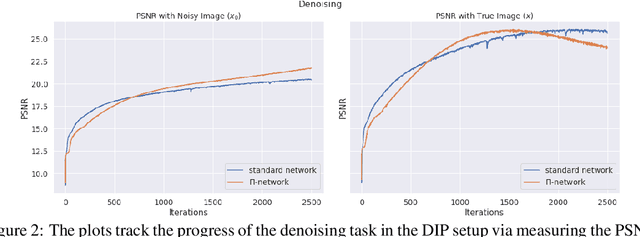
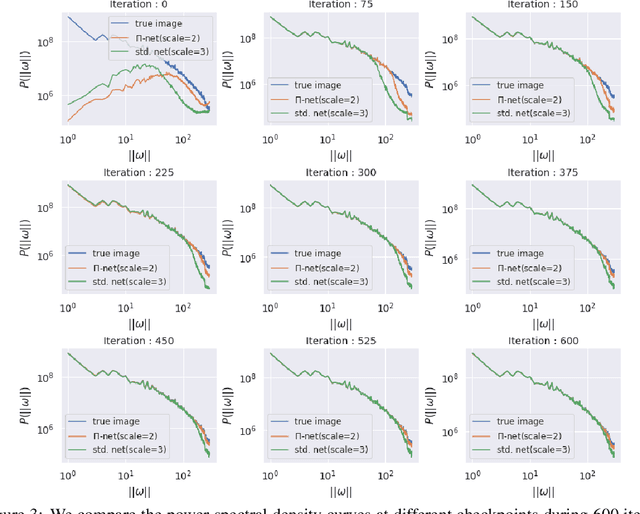
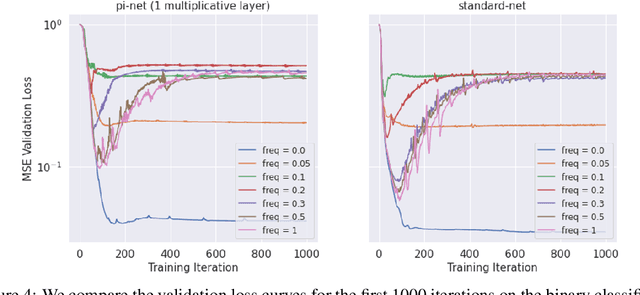
Polynomial neural networks (PNNs) have been recently shown to be particularly effective at image generation and face recognition, where high-frequency information is critical. Previous studies have revealed that neural networks demonstrate a $\textit{spectral bias}$ towards low-frequency functions, which yields faster learning of low-frequency components during training. Inspired by such studies, we conduct a spectral analysis of the Neural Tangent Kernel (NTK) of PNNs. We find that the $\Pi$-Net family, i.e., a recently proposed parametrization of PNNs, speeds up the learning of the higher frequencies. We verify the theoretical bias through extensive experiments. We expect our analysis to provide novel insights into designing architectures and learning frameworks by incorporating multiplicative interactions via polynomials.