PolyGAN: High-Order Polynomial Generators
Paper and Code
Aug 19, 2019
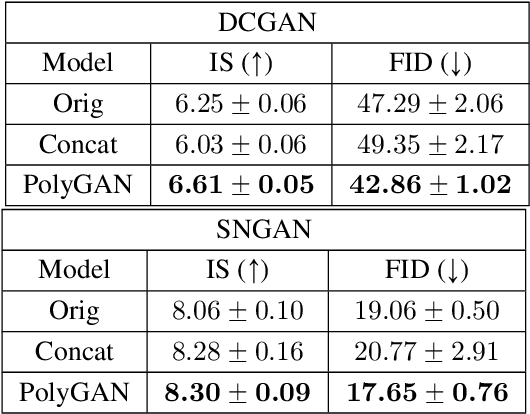
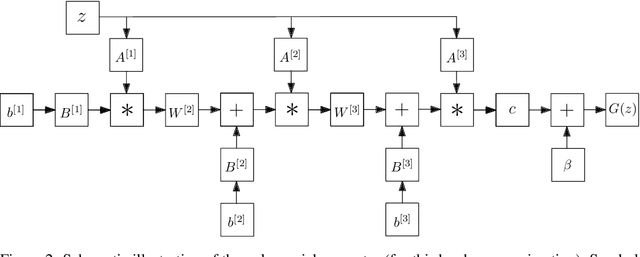

Generative Adversarial Networks (GANs) have become the gold standard when it comes to learning generative models that can describe intricate, high-dimensional distributions. Since their advent, numerous variations of GANs have been introduced in the literature, primarily focusing on utilization of novel loss functions, optimization/regularization strategies and architectures. In this work, we take an orthogonal approach to the above and turn our attention to the generator. We propose to model the data generator by means of a high-order polynomial using tensorial factors. We design a hierarchical decomposition of the polynomial and demonstrate how it can be efficiently implemented by a neural network. We show, for the first time, that by using our decomposition a GAN generator can approximate the data distribution by only using linear/convolution blocks without using any activation functions. Finally, we highlight that PolyGAN can be easily adapted and used along-side all major GAN architectures. In an extensive series of quantitative and qualitative experiments, PolyGAN improves upon the state-of-the-art by a significant margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge