Aligning Attention with Human Rationales for Self-Explaining Hate Speech Detection

The opaque nature of deep learning models presents significant challenges for the ethical deployment of hate speech detection systems. To address this limitation, we introduce Supervised Rational Attention (SRA), a framework that explicitly aligns model attention with human rationales, improving both interpretability and fairness in hate speech classification. SRA integrates a supervised attention mechanism into transformer-based classifiers, optimizing a joint objective that combines standard classification loss with an alignment loss term that minimizes the discrepancy between attention weights and human-annotated rationales. We evaluated SRA on hate speech benchmarks in English (HateXplain) and Portuguese (HateBRXplain) with rationale annotations. Empirically, SRA achieves 2.4x better explainability compared to current baselines, and produces token-level explanations that are more faithful and human-aligned. In terms of fairness, SRA achieves competitive fairness across all measures, with second-best performance in detecting toxic posts targeting identity groups, while maintaining comparable results on other metrics. These findings demonstrate that incorporating human rationales into attention mechanisms can enhance interpretability and faithfulness without compromising fairness.

Layer-wise Quantization for Quantized Optimistic Dual Averaging

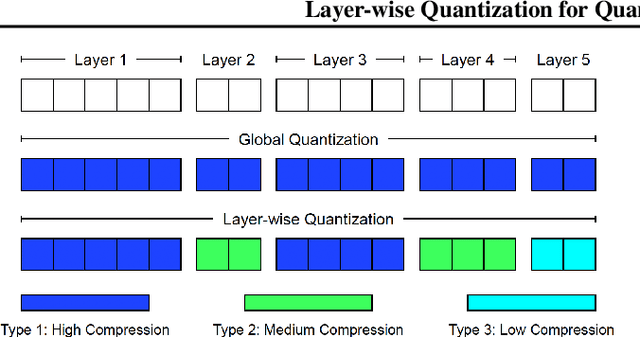
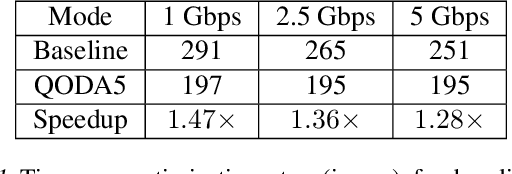
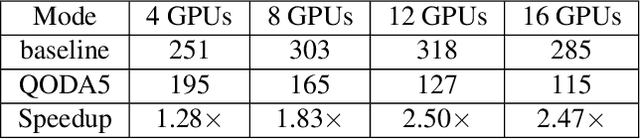
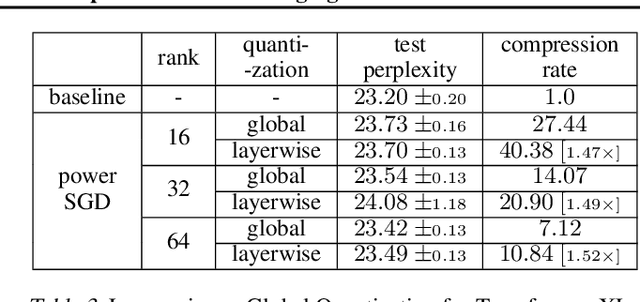
Modern deep neural networks exhibit heterogeneity across numerous layers of various types such as residuals, multi-head attention, etc., due to varying structures (dimensions, activation functions, etc.), distinct representation characteristics, which impact predictions. We develop a general layer-wise quantization framework with tight variance and code-length bounds, adapting to the heterogeneities over the course of training. We then apply a new layer-wise quantization technique within distributed variational inequalities (VIs), proposing a novel Quantized Optimistic Dual Averaging (QODA) algorithm with adaptive learning rates, which achieves competitive convergence rates for monotone VIs. We empirically show that QODA achieves up to a $150\%$ speedup over the baselines in end-to-end training time for training Wasserstein GAN on $12+$ GPUs.

Addressing Label Shift in Distributed Learning via Entropy Regularization

We address the challenge of minimizing true risk in multi-node distributed learning. These systems are frequently exposed to both inter-node and intra-node label shifts, which present a critical obstacle to effectively optimizing model performance while ensuring that data remains confined to each node. To tackle this, we propose the Versatile Robust Label Shift (VRLS) method, which enhances the maximum likelihood estimation of the test-to-train label density ratio. VRLS incorporates Shannon entropy-based regularization and adjusts the density ratio during training to better handle label shifts at the test time. In multi-node learning environments, VRLS further extends its capabilities by learning and adapting density ratios across nodes, effectively mitigating label shifts and improving overall model performance. Experiments conducted on MNIST, Fashion MNIST, and CIFAR-10 demonstrate the effectiveness of VRLS, outperforming baselines by up to 20% in imbalanced settings. These results highlight the significant improvements VRLS offers in addressing label shifts. Our theoretical analysis further supports this by establishing high-probability bounds on estimation errors.

Distributed Extra-gradient with Optimal Complexity and Communication Guarantees

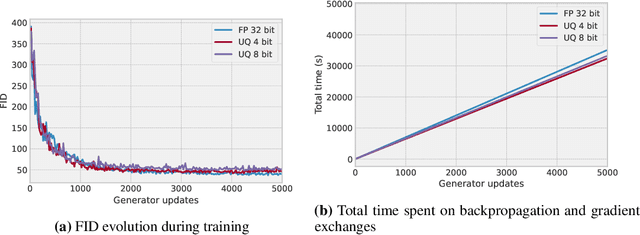
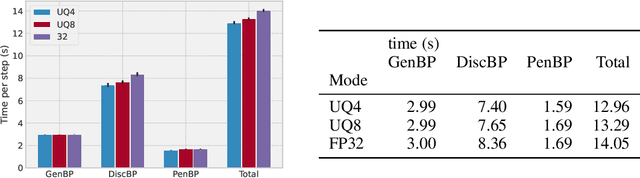
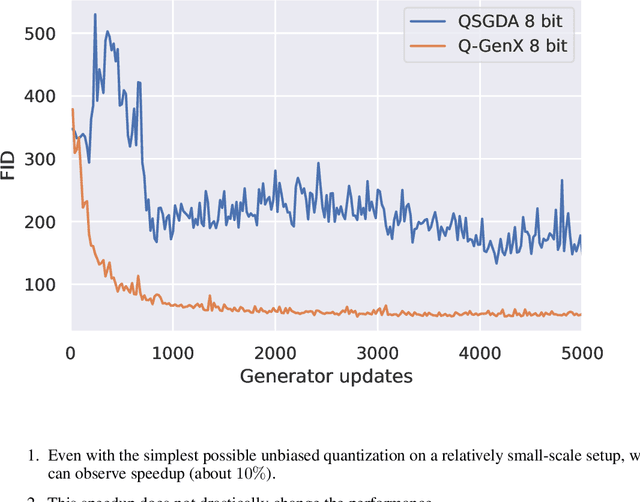
We consider monotone variational inequality (VI) problems in multi-GPU settings where multiple processors/workers/clients have access to local stochastic dual vectors. This setting includes a broad range of important problems from distributed convex minimization to min-max and games. Extra-gradient, which is a de facto algorithm for monotone VI problems, has not been designed to be communication-efficient. To this end, we propose a quantized generalized extra-gradient (Q-GenX), which is an unbiased and adaptive compression method tailored to solve VIs. We provide an adaptive step-size rule, which adapts to the respective noise profiles at hand and achieve a fast rate of ${\mathcal O}(1/T)$ under relative noise, and an order-optimal ${\mathcal O}(1/\sqrt{T})$ under absolute noise and show distributed training accelerates convergence. Finally, we validate our theoretical results by providing real-world experiments and training generative adversarial networks on multiple GPUs.

Federated Learning under Covariate Shifts with Generalization Guarantees

This paper addresses intra-client and inter-client covariate shifts in federated learning (FL) with a focus on the overall generalization performance. To handle covariate shifts, we formulate a new global model training paradigm and propose Federated Importance-Weighted Empirical Risk Minimization (FTW-ERM) along with improving density ratio matching methods without requiring perfect knowledge of the supremum over true ratios. We also propose the communication-efficient variant FITW-ERM with the same level of privacy guarantees as those of classical ERM in FL. We theoretically show that FTW-ERM achieves smaller generalization error than classical ERM under certain settings. Experimental results demonstrate the superiority of FTW-ERM over existing FL baselines in challenging imbalanced federated settings in terms of data distribution shifts across clients.

MixTailor: Mixed Gradient Aggregation for Robust Learning Against Tailored Attacks

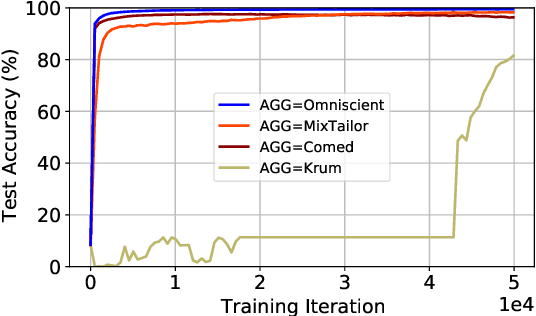
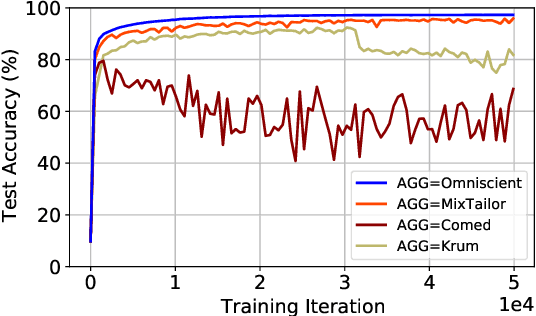
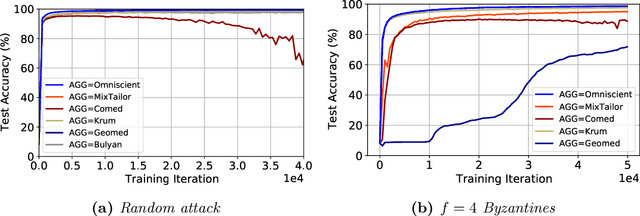
Implementations of SGD on distributed and multi-GPU systems creates new vulnerabilities, which can be identified and misused by one or more adversarial agents. Recently, it has been shown that well-known Byzantine-resilient gradient aggregation schemes are indeed vulnerable to informed attackers that can tailor the attacks (Fang et al., 2020; Xie et al., 2020b). We introduce MixTailor, a scheme based on randomization of the aggregation strategies that makes it impossible for the attacker to be fully informed. Deterministic schemes can be integrated into MixTailor on the fly without introducing any additional hyperparameters. Randomization decreases the capability of a powerful adversary to tailor its attacks, while the resulting randomized aggregation scheme is still competitive in terms of performance. For both iid and non-iid settings, we establish almost sure convergence guarantees that are both stronger and more general than those available in the literature. Our empirical studies across various datasets, attacks, and settings, validate our hypothesis and show that MixTailor successfully defends when well-known Byzantine-tolerant schemes fail.

Subquadratic Overparameterization for Shallow Neural Networks

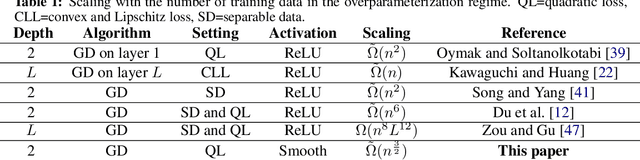
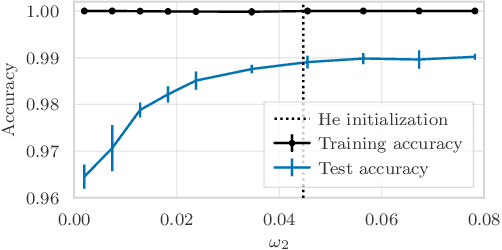
Overparameterization refers to the important phenomenon where the width of a neural network is chosen such that learning algorithms can provably attain zero loss in nonconvex training. The existing theory establishes such global convergence using various initialization strategies, training modifications, and width scalings. In particular, the state-of-the-art results require the width to scale quadratically with the number of training data under standard initialization strategies used in practice for best generalization performance. In contrast, the most recent results obtain linear scaling either with requiring initializations that lead to the "lazy-training", or training only a single layer. In this work, we provide an analytical framework that allows us to adopt standard initialization strategies, possibly avoid lazy training, and train all layers simultaneously in basic shallow neural networks while attaining a desirable subquadratic scaling on the network width. We achieve the desiderata via Polyak-Lojasiewicz condition, smoothness, and standard assumptions on data, and use tools from random matrix theory.

NUQSGD: Provably Communication-efficient Data-parallel SGD via Nonuniform Quantization

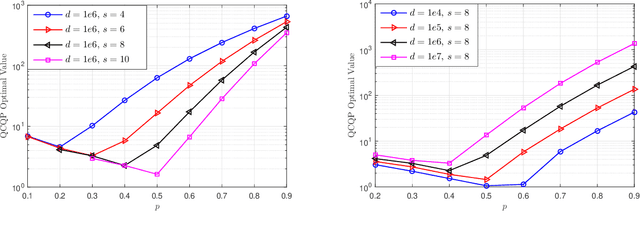
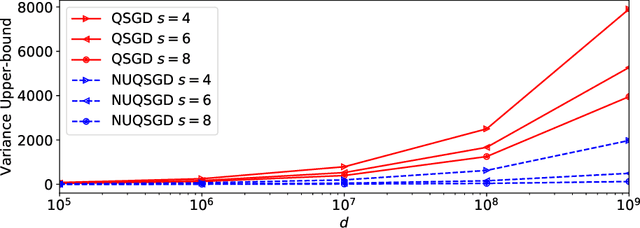
As the size and complexity of models and datasets grow, so does the need for communication-efficient variants of stochastic gradient descent that can be deployed to perform parallel model training. One popular communication-compression method for data-parallel SGD is QSGD (Alistarh et al., 2017), which quantizes and encodes gradients to reduce communication costs. The baseline variant of QSGD provides strong theoretical guarantees, however, for practical purposes, the authors proposed a heuristic variant which we call QSGDinf, which demonstrated impressive empirical gains for distributed training of large neural networks. In this paper, we build on this work to propose a new gradient quantization scheme, and show that it has both stronger theoretical guarantees than QSGD, and matches and exceeds the empirical performance of the QSGDinf heuristic and of other compression methods.

On the Generalization of Stochastic Gradient Descent with Momentum

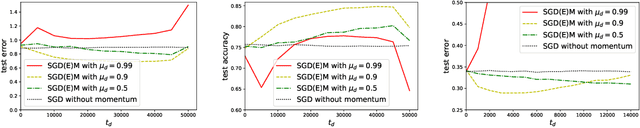
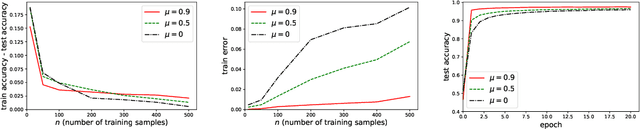
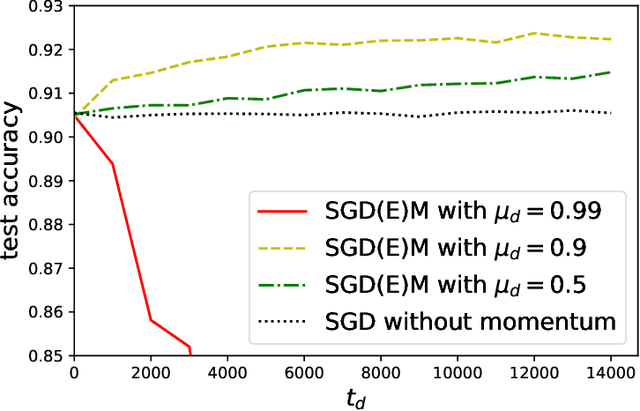
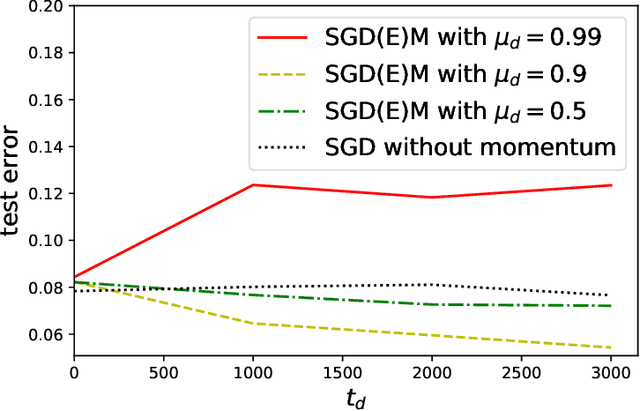
While momentum-based methods, in conjunction with stochastic gradient descent (SGD), are widely used when training machine learning models, there is little theoretical understanding on the generalization error of such methods. In this work, we first show that there exists a convex loss function for which algorithmic stability fails to establish generalization guarantees when SGD with standard heavy-ball momentum (SGDM) is run for multiple epochs. Then, for smooth Lipschitz loss functions, we analyze a modified momentum-based update rule, i.e., SGD with early momentum (SGDEM), and show that it admits an upper-bound on the generalization error. Thus, our results show that machine learning models can be trained for multiple epochs of SGDEM with a guarantee for generalization. Finally, for the special case of strongly convex loss functions, we find a range of momentum such that multiple epochs of standard SGDM, as a special form of SGDEM, also generalizes. Extending our results on generalization, we also develop an upper-bound on the expected true risk, in terms of the number of training steps, the size of the training set, and the momentum parameter. Experimental evaluations verify the consistency between the numerical results and our theoretical bounds and the effectiveness of SGDEM for smooth Lipschitz loss functions.

Adaptive Gradient Quantization for Data-Parallel SGD

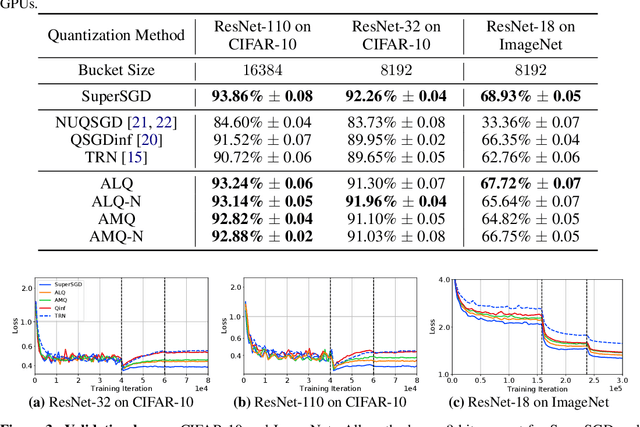
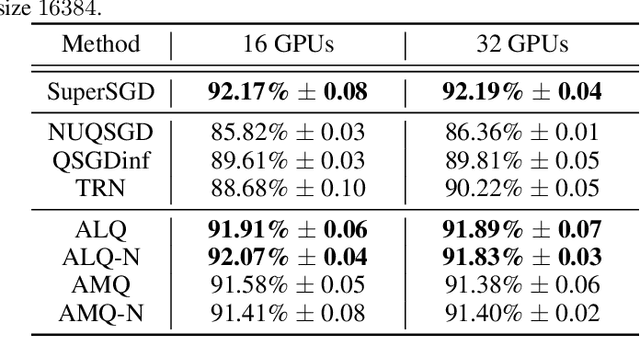
Many communication-efficient variants of SGD use gradient quantization schemes. These schemes are often heuristic and fixed over the course of training. We empirically observe that the statistics of gradients of deep models change during the training. Motivated by this observation, we introduce two adaptive quantization schemes, ALQ and AMQ. In both schemes, processors update their compression schemes in parallel by efficiently computing sufficient statistics of a parametric distribution. We improve the validation accuracy by almost 2% on CIFAR-10 and 1% on ImageNet in challenging low-cost communication setups. Our adaptive methods are also significantly more robust to the choice of hyperparameters.