On the Generalization of Stochastic Gradient Descent with Momentum
Paper and Code
Feb 26, 2021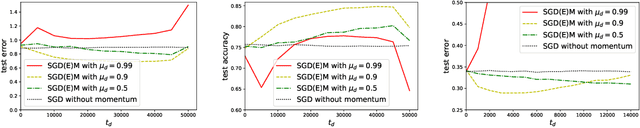
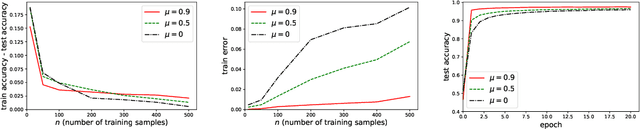
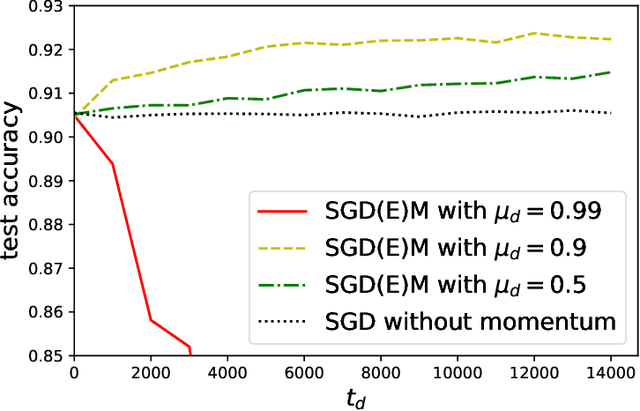
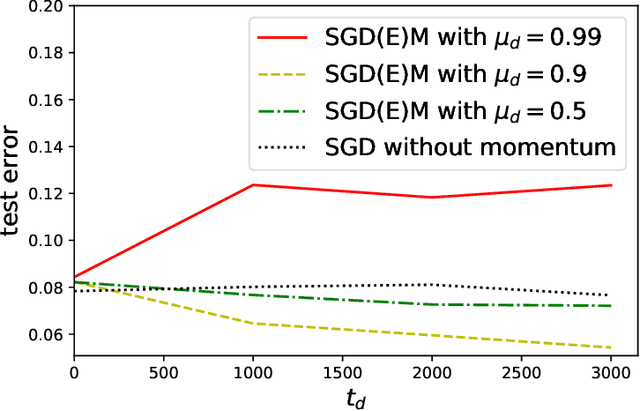
While momentum-based methods, in conjunction with stochastic gradient descent (SGD), are widely used when training machine learning models, there is little theoretical understanding on the generalization error of such methods. In this work, we first show that there exists a convex loss function for which algorithmic stability fails to establish generalization guarantees when SGD with standard heavy-ball momentum (SGDM) is run for multiple epochs. Then, for smooth Lipschitz loss functions, we analyze a modified momentum-based update rule, i.e., SGD with early momentum (SGDEM), and show that it admits an upper-bound on the generalization error. Thus, our results show that machine learning models can be trained for multiple epochs of SGDEM with a guarantee for generalization. Finally, for the special case of strongly convex loss functions, we find a range of momentum such that multiple epochs of standard SGDM, as a special form of SGDEM, also generalizes. Extending our results on generalization, we also develop an upper-bound on the expected true risk, in terms of the number of training steps, the size of the training set, and the momentum parameter. Experimental evaluations verify the consistency between the numerical results and our theoretical bounds and the effectiveness of SGDEM for smooth Lipschitz loss functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge