Over-Parametrized Matrix Factorization in the Presence of Spurious Stationary Points

Motivated by the emerging role of interpolating machines in signal processing and machine learning, this work considers the computational aspects of over-parametrized matrix factorization. In this context, the optimization landscape may contain spurious stationary points (SSPs), which are proved to be full-rank matrices. The presence of these SSPs means that it is impossible to hope for any global guarantees in over-parametrized matrix factorization. For example, when initialized at an SSP, the gradient flow will be trapped there forever. Nevertheless, despite these SSPs, we establish in this work that the gradient flow of the corresponding merit function converges to a global minimizer, provided that its initialization is rank-deficient and sufficiently close to the feasible set of the optimization problem. We numerically observe that a heuristic discretization of the proposed gradient flow, inspired by primal-dual algorithms, is successful when initialized randomly. Our result is in sharp contrast with the local refinement methods which require an initialization close to the optimal set of the optimization problem. More specifically, we successfully avoid the traps set by the SSPs because the gradient flow remains rank-deficient at all times, and not because there are no SSPs nearby. The latter is the case for the local refinement methods. Moreover, the widely-used restricted isometry property plays no role in our main result.

Subquadratic Overparameterization for Shallow Neural Networks

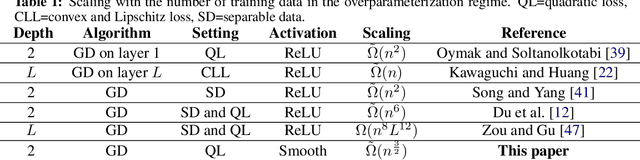
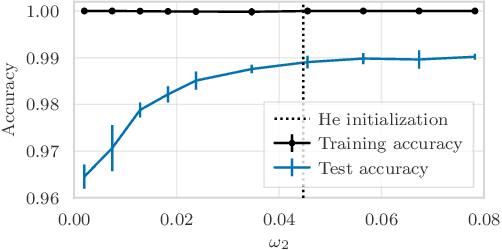
Overparameterization refers to the important phenomenon where the width of a neural network is chosen such that learning algorithms can provably attain zero loss in nonconvex training. The existing theory establishes such global convergence using various initialization strategies, training modifications, and width scalings. In particular, the state-of-the-art results require the width to scale quadratically with the number of training data under standard initialization strategies used in practice for best generalization performance. In contrast, the most recent results obtain linear scaling either with requiring initializations that lead to the "lazy-training", or training only a single layer. In this work, we provide an analytical framework that allows us to adopt standard initialization strategies, possibly avoid lazy training, and train all layers simultaneously in basic shallow neural networks while attaining a desirable subquadratic scaling on the network width. We achieve the desiderata via Polyak-Lojasiewicz condition, smoothness, and standard assumptions on data, and use tools from random matrix theory.

Nonlinear matrix recovery using optimization on the Grassmann manifold

We investigate the problem of recovering a partially observed high-rank matrix whose columns obey a nonlinear structure such as a union of subspaces, an algebraic variety or grouped in clusters. The recovery problem is formulated as the rank minimization of a nonlinear feature map applied to the original matrix, which is then further approximated by a constrained non-convex optimization problem involving the Grassmann manifold. We propose two sets of algorithms, one arising from Riemannian optimization and the other as an alternating minimization scheme, both of which include first- and second-order variants. Both sets of algorithms have theoretical guarantees. In particular, for the alternating minimization, we establish global convergence and worst-case complexity bounds. Additionally, using the Kurdyka-Lojasiewicz property, we show that the alternating minimization converges to a unique limit point. We provide extensive numerical results for the recovery of union of subspaces and clustering under entry sampling and dense Gaussian sampling. Our methods are competitive with existing approaches and, in particular, high accuracy is achieved in the recovery using Riemannian second-order methods.

Principal Component Hierarchy for Sparse Quadratic Programs

We propose a novel approximation hierarchy for cardinality-constrained, convex quadratic programs that exploits the rank-dominating eigenvectors of the quadratic matrix. Each level of approximation admits a min-max characterization whose objective function can be optimized over the binary variables analytically, while preserving convexity in the continuous variables. Exploiting this property, we propose two scalable optimization algorithms, coined as the "best response" and the "dual program", that can efficiently screen the potential indices of the nonzero elements of the original program. We show that the proposed methods are competitive with the existing screening methods in the current sparse regression literature, and it is particularly fast on instances with high number of measurements in experiments with both synthetic and real datasets.

The Nonconvex Geometry of Linear Inverse Problems

The gauge function, closely related to the atomic norm, measures the complexity of a statistical model, and has found broad applications in machine learning and statistical signal processing. In a high-dimensional learning problem, the gauge function attempts to safeguard against overfitting by promoting a sparse (concise) representation within the learning alphabet. In this work, within the context of linear inverse problems, we pinpoint the source of its success, but also argue that the applicability of the gauge function is inherently limited by its convexity, and showcase several learning problems where the classical gauge function theory fails. We then introduce a new notion of statistical complexity, gauge$_p$ function, which overcomes the limitations of the gauge function. The gauge$_p$ function is a simple generalization of the gauge function that can tightly control the sparsity of a statistical model within the learning alphabet and, perhaps surprisingly, draws further inspiration from the Burer-Monteiro factorization in computational mathematics. We also propose a new learning machine, with the building block of gauge$_p$ function, and arm this machine with a number of statistical guarantees. The potential of the proposed gauge$_p$ function theory is then studied for two stylized applications. Finally, we discuss the computational aspects and, in particular, suggest a tractable numerical algorithm for implementing the new learning machine.

Nearly Minimal Over-Parametrization of Shallow Neural Networks

A recent line of work has shown that an overparametrized neural network can perfectly fit the training data, an otherwise often intractable nonconvex optimization problem. For (fully-connected) shallow networks, in the best case scenario, the existing theory requires quadratic over-parametrization as a function of the number of training samples. This paper establishes that linear overparametrization is sufficient to fit the training data, using a simple variant of the (stochastic) gradient descent. Crucially, unlike several related works, the training considered in this paper is not limited to the lazy regime in the sense cautioned against in [1, 2]. Beyond shallow networks, the framework developed in this work for over-parametrization is applicable to a variety of learning problems.

Fast and Provable ADMM for Learning with Generative Priors

In this work, we propose a (linearized) Alternating Direction Method-of-Multipliers (ADMM) algorithm for minimizing a convex function subject to a nonconvex constraint. We focus on the special case where such constraint arises from the specification that a variable should lie in the range of a neural network. This is motivated by recent successful applications of Generative Adversarial Networks (GANs) in tasks like compressive sensing, denoising and robustness against adversarial examples. The derived rates for our algorithm are characterized in terms of certain geometric properties of the generator network, which we show hold for feedforward architectures, under mild assumptions. Unlike gradient descent (GD), it can efficiently handle non-smooth objectives as well as exploit efficient partial minimization procedures, thus being faster in many practical scenarios.