SOLBP: Second-Order Loopy Belief Propagation for Inference in Uncertain Bayesian Networks

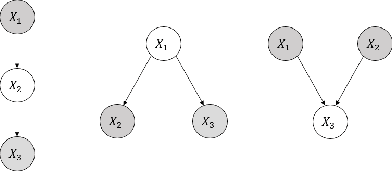
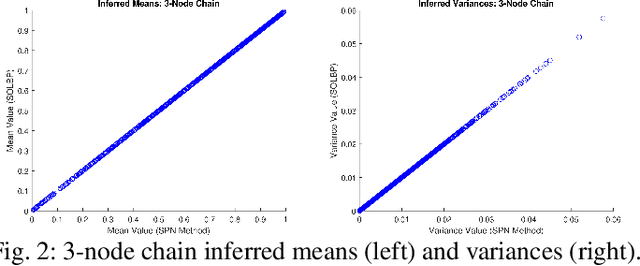
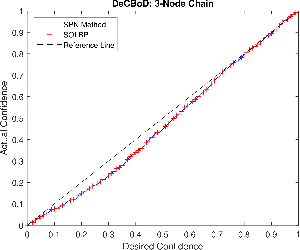
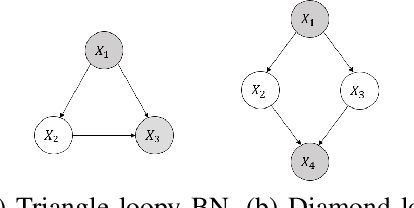
In second-order uncertain Bayesian networks, the conditional probabilities are only known within distributions, i.e., probabilities over probabilities. The delta-method has been applied to extend exact first-order inference methods to propagate both means and variances through sum-product networks derived from Bayesian networks, thereby characterizing epistemic uncertainty, or the uncertainty in the model itself. Alternatively, second-order belief propagation has been demonstrated for polytrees but not for general directed acyclic graph structures. In this work, we extend Loopy Belief Propagation to the setting of second-order Bayesian networks, giving rise to Second-Order Loopy Belief Propagation (SOLBP). For second-order Bayesian networks, SOLBP generates inferences consistent with those generated by sum-product networks, while being more computationally efficient and scalable.

Aggregating Probabilistic Judgments

In this paper we explore the application of methods for classical judgment aggregation in pooling probabilistic opinions on logically related issues. For this reason, we first modify the Boolean judgment aggregation framework in the way that allows handling probabilistic judgments and then define probabilistic aggregation functions obtained by generalization of the classical ones. In addition, we discuss essential desirable properties for the aggregation functions and explore impossibility results.

Counterfactually Fair Prediction Using Multiple Causal Models

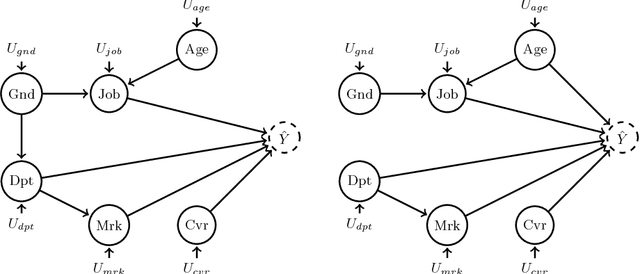
In this paper we study the problem of making predictions using multiple structural casual models defined by different agents, under the constraint that the prediction satisfies the criterion of counterfactual fairness. Relying on the frameworks of causality, fairness and opinion pooling, we build upon and extend previous work focusing on the qualitative aggregation of causal Bayesian networks and causal models. In order to complement previous qualitative results, we devise a method based on Monte Carlo simulations. This method enables a decision-maker to aggregate the outputs of the causal models provided by different experts while guaranteeing the counterfactual fairness of the result. We demonstrate our approach on a simple, yet illustrative, toy case study.

Pooling of Causal Models under Counterfactual Fairness via Causal Judgement Aggregation

In this paper we consider the problem of combining multiple probabilistic causal models, provided by different experts, under the requirement that the aggregated model satisfy the criterion of counterfactual fairness. We build upon the work on causal models and fairness in machine learning, and we express the problem of combining multiple models within the framework of opinion pooling. We propose two simple algorithms, grounded in the theory of counterfactual fairness and causal judgment aggregation, that are guaranteed to generate aggregated probabilistic causal models respecting the criterion of fairness, and we compare their behaviors on a toy case study.