SOLBP: Second-Order Loopy Belief Propagation for Inference in Uncertain Bayesian Networks

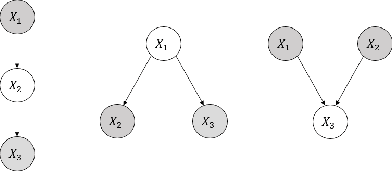
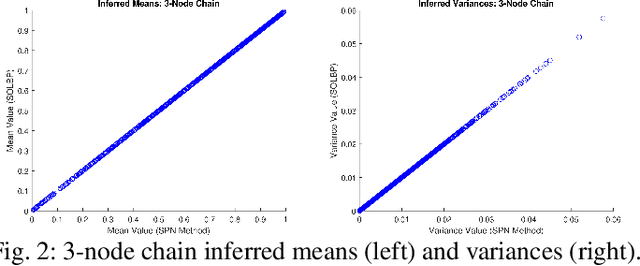
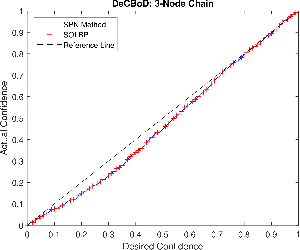
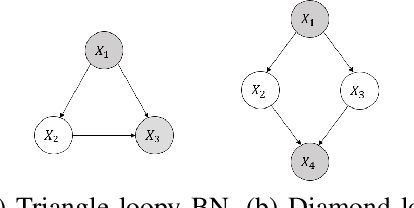
In second-order uncertain Bayesian networks, the conditional probabilities are only known within distributions, i.e., probabilities over probabilities. The delta-method has been applied to extend exact first-order inference methods to propagate both means and variances through sum-product networks derived from Bayesian networks, thereby characterizing epistemic uncertainty, or the uncertainty in the model itself. Alternatively, second-order belief propagation has been demonstrated for polytrees but not for general directed acyclic graph structures. In this work, we extend Loopy Belief Propagation to the setting of second-order Bayesian networks, giving rise to Second-Order Loopy Belief Propagation (SOLBP). For second-order Bayesian networks, SOLBP generates inferences consistent with those generated by sum-product networks, while being more computationally efficient and scalable.

Uncertain Bayesian Networks: Learning from Incomplete Data

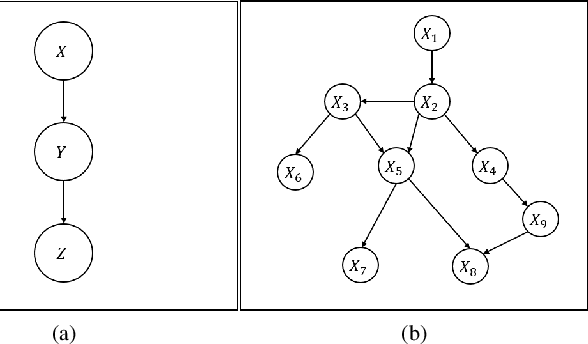
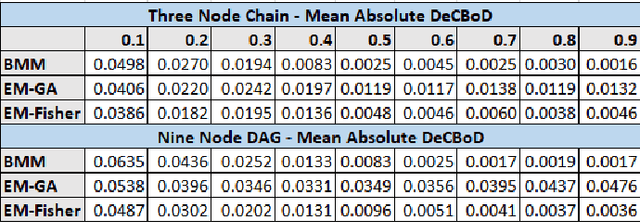
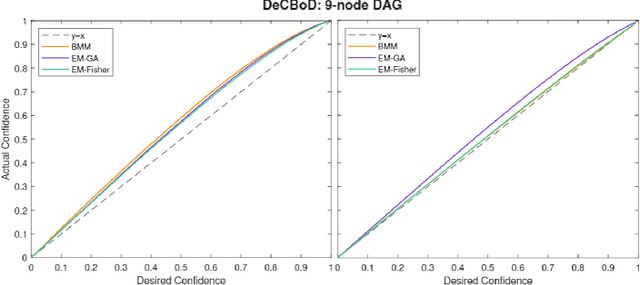
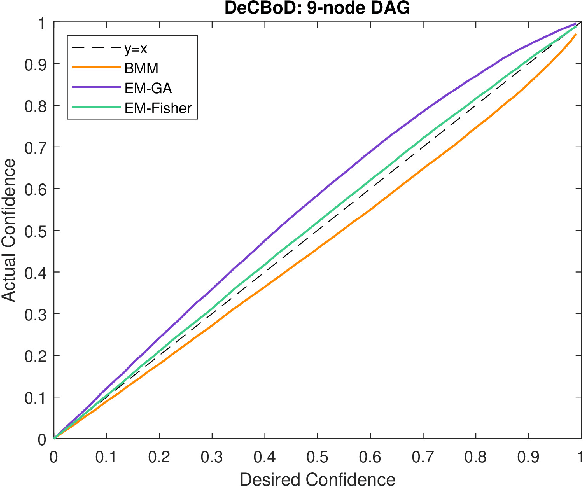
When the historical data are limited, the conditional probabilities associated with the nodes of Bayesian networks are uncertain and can be empirically estimated. Second order estimation methods provide a framework for both estimating the probabilities and quantifying the uncertainty in these estimates. We refer to these cases as uncer tain or second-order Bayesian networks. When such data are complete, i.e., all variable values are observed for each instantiation, the conditional probabilities are known to be Dirichlet-distributed. This paper improves the current state-of-the-art approaches for handling uncertain Bayesian networks by enabling them to learn distributions for their parameters, i.e., conditional probabilities, with incomplete data. We extensively evaluate various methods to learn the posterior of the parameters through the desired and empirically derived strength of confidence bounds for various queries.