A Differentially Private Weighted Empirical Risk Minimization Procedure and its Application to Outcome Weighted Learning

It is commonplace to use data containing personal information to build predictive models in the framework of empirical risk minimization (ERM). While these models can be highly accurate in prediction, results obtained from these models with the use of sensitive data may be susceptible to privacy attacks. Differential privacy (DP) is an appealing framework for addressing such data privacy issues by providing mathematically provable bounds on the privacy loss incurred when releasing information from sensitive data. Previous work has primarily concentrated on applying DP to unweighted ERM. We consider an important generalization to weighted ERM (wERM). In wERM, each individual's contribution to the objective function can be assigned varying weights. In this context, we propose the first differentially private wERM algorithm, backed by a rigorous theoretical proof of its DP guarantees under mild regularity conditions. Extending the existing DP-ERM procedures to wERM paves a path to deriving privacy-preserving learning methods for individualized treatment rules, including the popular outcome weighted learning (OWL). We evaluate the performance of the DP-wERM application to OWL in a simulation study and in a real clinical trial of melatonin for sleep health. All empirical results demonstrate the viability of training OWL models via wERM with DP guarantees while maintaining sufficiently useful model performance. Therefore, we recommend practitioners consider implementing the proposed privacy-preserving OWL procedure in real-world scenarios involving sensitive data.

Robust High-Dimensional Regression with Coefficient Thresholding and its Application to Imaging Data Analysis

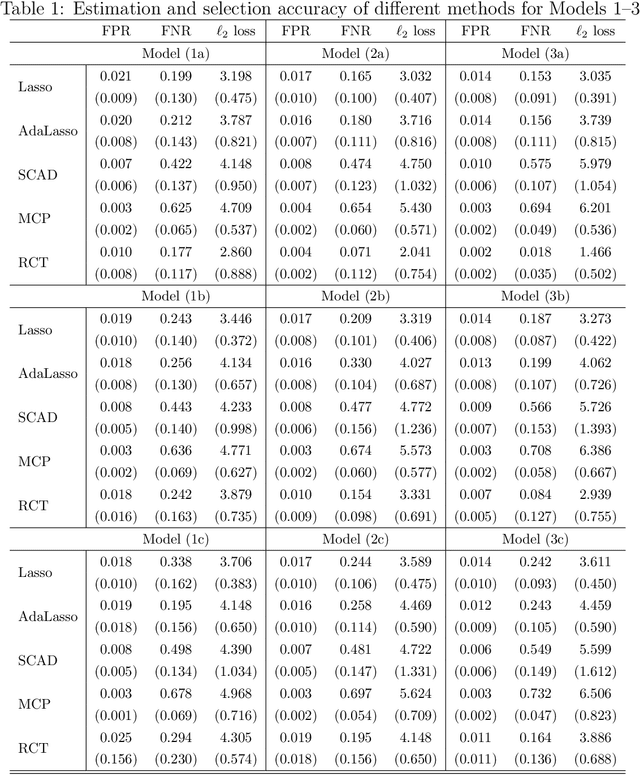
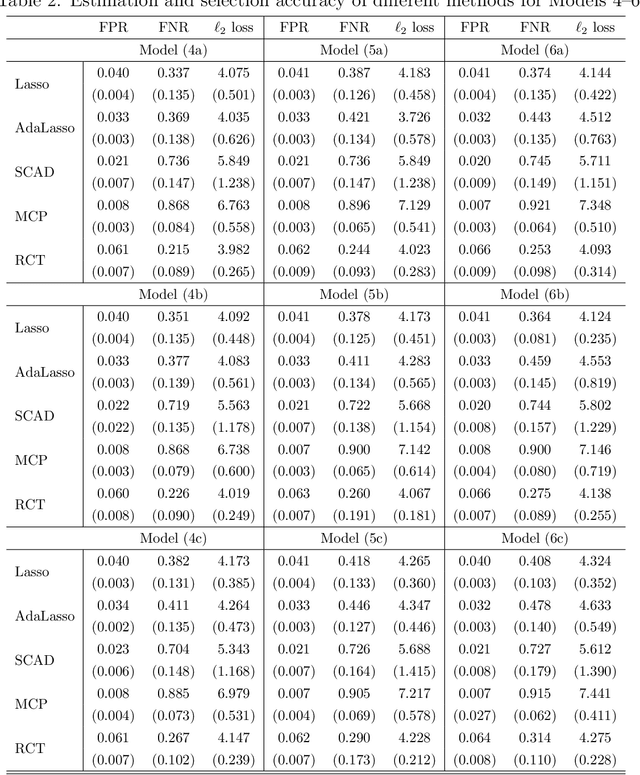
It is of importance to develop statistical techniques to analyze high-dimensional data in the presence of both complex dependence and possible outliers in real-world applications such as imaging data analyses. We propose a new robust high-dimensional regression with coefficient thresholding, in which an efficient nonconvex estimation procedure is proposed through a thresholding function and the robust Huber loss. The proposed regularization method accounts for complex dependence structures in predictors and is robust against outliers in outcomes. Theoretically, we analyze rigorously the landscape of the population and empirical risk functions for the proposed method. The fine landscape enables us to establish both {statistical consistency and computational convergence} under the high-dimensional setting. The finite-sample properties of the proposed method are examined by extensive simulation studies. An illustration of real-world application concerns a scalar-on-image regression analysis for an association of psychiatric disorder measured by the general factor of psychopathology with features extracted from the task functional magnetic resonance imaging data in the Adolescent Brain Cognitive Development study.

Data Discovery Using Lossless Compression-Based Sparse Representation

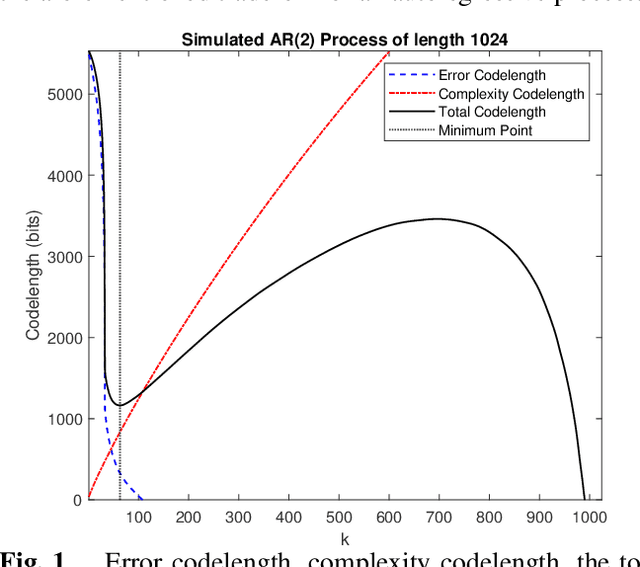
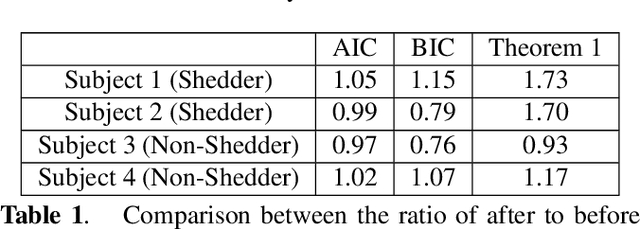
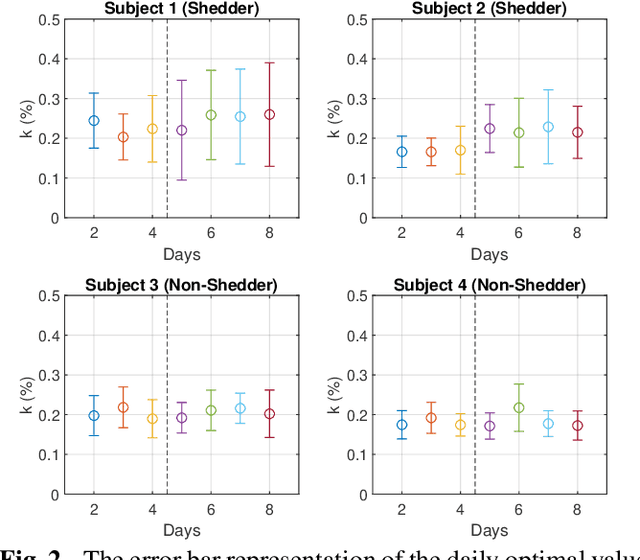
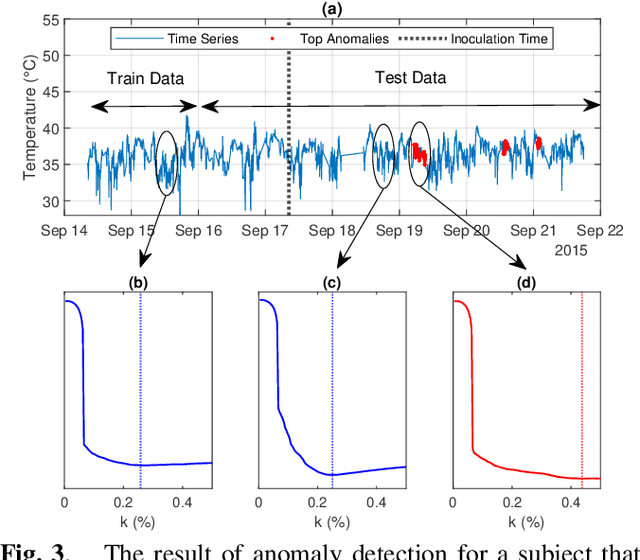
Sparse representation has been widely used in data compression, signal and image denoising, dimensionality reduction and computer vision. While overcomplete dictionaries are required for sparse representation of multidimensional data, orthogonal bases represent one-dimensional data well. In this paper, we propose a data-driven sparse representation using orthonormal bases under the lossless compression constraint. We show that imposing such constraint under the Minimum Description Length (MDL) principle leads to a unique and optimal sparse representation for one-dimensional data, which results in discriminative features useful for data discovery.