Data Discovery Using Lossless Compression-Based Sparse Representation
Paper and Code
Mar 17, 2021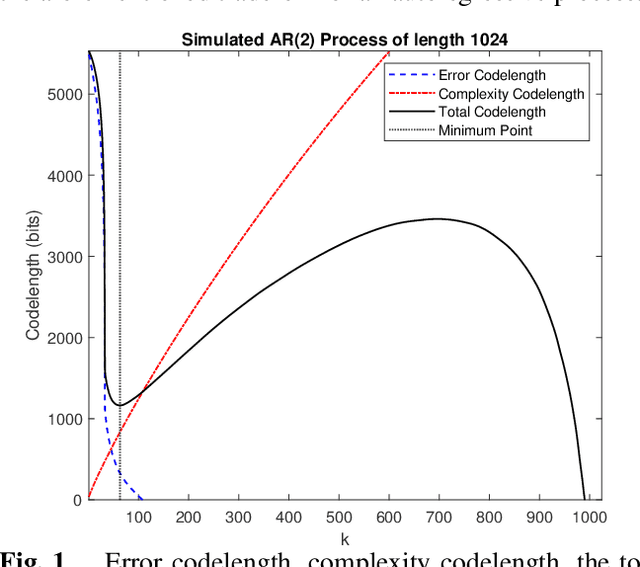
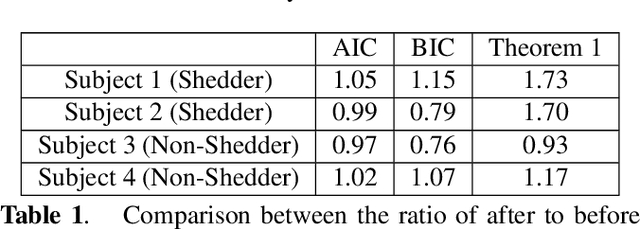
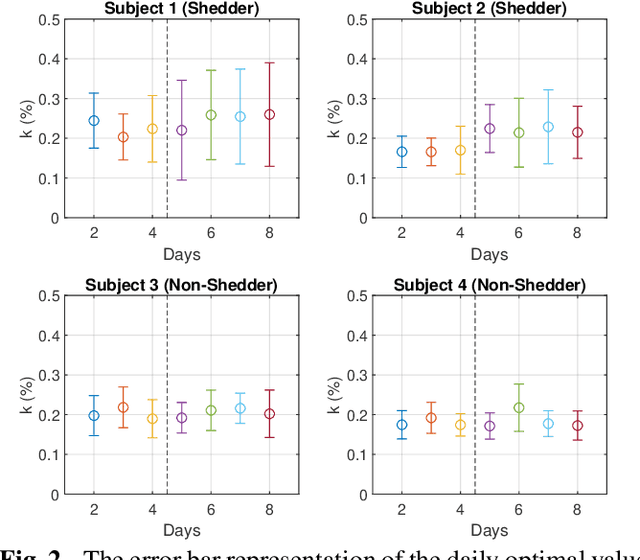
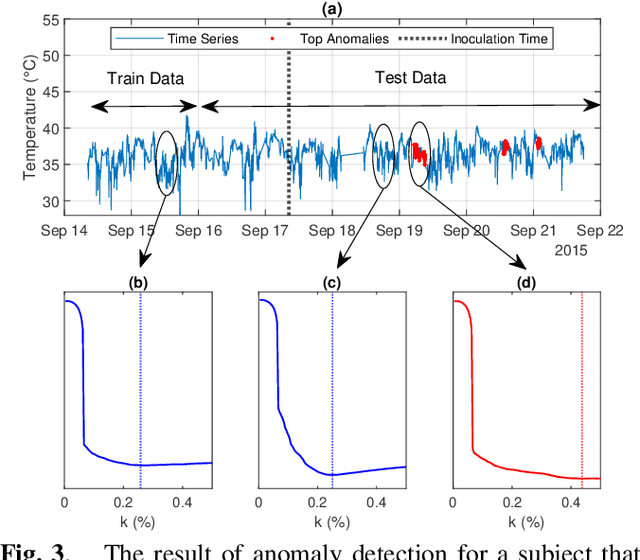
Sparse representation has been widely used in data compression, signal and image denoising, dimensionality reduction and computer vision. While overcomplete dictionaries are required for sparse representation of multidimensional data, orthogonal bases represent one-dimensional data well. In this paper, we propose a data-driven sparse representation using orthonormal bases under the lossless compression constraint. We show that imposing such constraint under the Minimum Description Length (MDL) principle leads to a unique and optimal sparse representation for one-dimensional data, which results in discriminative features useful for data discovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge