High-Dimensional Sequential Change Detection

We address the problem of detecting a change in the distribution of a high-dimensional multivariate normal time series. Assuming that the post-change parameters are unknown and estimated using a window of historical data, we extend the framework of quickest change detection (QCD) to the highdimensional setting in which the number of variables increases proportionally with the size of the window used to estimate the post-change parameters. Our analysis reveals that an information theoretic quantity, which we call the Normalized High- Dimensional Kullback-Leibler divergence (NHDKL), governs the high-dimensional asymptotic performance of QCD procedures. Specifically, we show that the detection delay is asymptotically inversely proportional to the difference between the NHDKL of the true post-change versus pre-change distributions and the NHDKL of the true versus estimated post-change distributions. In cases of perfect estimation, where the latter NHDKL is zero, the delay is inversely proportional to the NHDKL between the post-change and pre-change distributions alone. Thus, our analysis is a direct generalization of the traditional fixed-dimension, large-sample asymptotic framework, where the standard KL divergence is asymptotically inversely proportional to detection delay. Finally, we identify parameter estimators that asymptotically minimize the NHDKL between the true versus estimated post-change distributions, resulting in a QCD method that is guaranteed to outperform standard approaches based on fixed-dimension asymptotics.

Community Detection in High-Dimensional Graph Ensembles

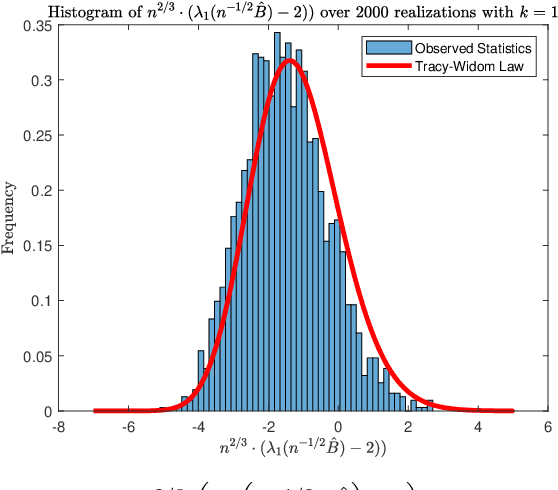
Detecting communities in high-dimensional graphs can be achieved by applying random matrix theory where the adjacency matrix of the graph is modeled by a Stochastic Block Model (SBM). However, the SBM makes an unrealistic assumption that the edge probabilities are homogeneous within communities, i.e., the edges occur with the same probabilities. The Degree-Corrected SBM is a generalization of the SBM that allows these edge probabilities to be different, but existing results from random matrix theory are not directly applicable to this heterogeneous model. In this paper, we derive a transformation of the adjacency matrix that eliminates this heterogeneity and preserves the relevant eigenstructure for community detection. We propose a test based on the extreme eigenvalues of this transformed matrix and (1) provide a method for controlling the significance level, (2) formulate a conjecture that the test achieves power one for all positive significance levels in the limit as the number of nodes approaches infinity, and (3) provide empirical evidence and theory supporting these claims.