Confidence-Constrained Maximum Entropy Framework for Learning from Multi-Instance Data
Paper and Code
Mar 07, 2016

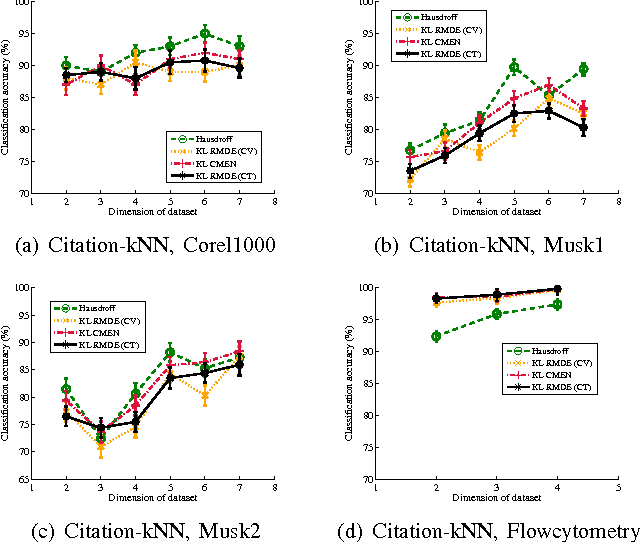

Multi-instance data, in which each object (bag) contains a collection of instances, are widespread in machine learning, computer vision, bioinformatics, signal processing, and social sciences. We present a maximum entropy (ME) framework for learning from multi-instance data. In this approach each bag is represented as a distribution using the principle of ME. We introduce the concept of confidence-constrained ME (CME) to simultaneously learn the structure of distribution space and infer each distribution. The shared structure underlying each density is used to learn from instances inside each bag. The proposed CME is free of tuning parameters. We devise a fast optimization algorithm capable of handling large scale multi-instance data. In the experimental section, we evaluate the performance of the proposed approach in terms of exact rank recovery in the space of distributions and compare it with the regularized ME approach. Moreover, we compare the performance of CME with Multi-Instance Learning (MIL) state-of-the-art algorithms and show a comparable performance in terms of accuracy with reduced computational complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge