Behrouz Behmardi
Confidence-Constrained Maximum Entropy Framework for Learning from Multi-Instance Data
Mar 07, 2016

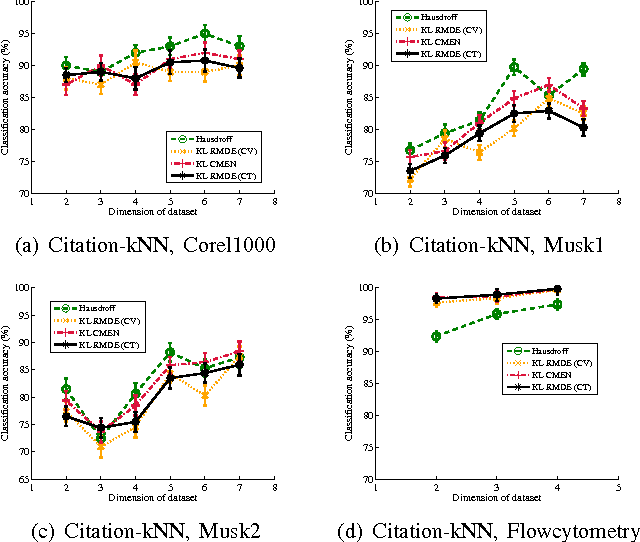

Abstract:Multi-instance data, in which each object (bag) contains a collection of instances, are widespread in machine learning, computer vision, bioinformatics, signal processing, and social sciences. We present a maximum entropy (ME) framework for learning from multi-instance data. In this approach each bag is represented as a distribution using the principle of ME. We introduce the concept of confidence-constrained ME (CME) to simultaneously learn the structure of distribution space and infer each distribution. The shared structure underlying each density is used to learn from instances inside each bag. The proposed CME is free of tuning parameters. We devise a fast optimization algorithm capable of handling large scale multi-instance data. In the experimental section, we evaluate the performance of the proposed approach in terms of exact rank recovery in the space of distributions and compare it with the regularized ME approach. Moreover, we compare the performance of CME with Multi-Instance Learning (MIL) state-of-the-art algorithms and show a comparable performance in terms of accuracy with reduced computational complexity.
Overlapping Trace Norms in Multi-View Learning
Apr 27, 2014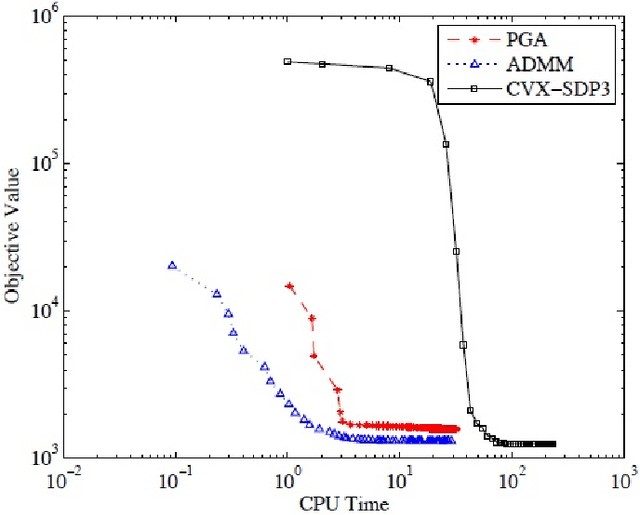
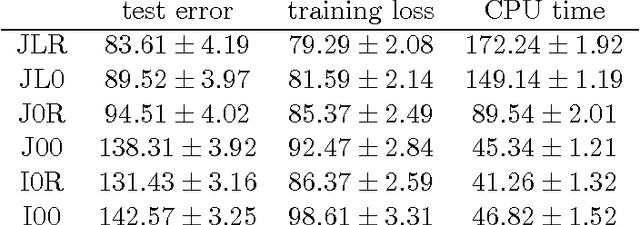

Abstract:Multi-view learning leverages correlations between different sources of data to make predictions in one view based on observations in another view. A popular approach is to assume that, both, the correlations between the views and the view-specific covariances have a low-rank structure, leading to inter-battery factor analysis, a model closely related to canonical correlation analysis. We propose a convex relaxation of this model using structured norm regularization. Further, we extend the convex formulation to a robust version by adding an l1-penalized matrix to our estimator, similarly to convex robust PCA. We develop and compare scalable algorithms for several convex multi-view models. We show experimentally that the view-specific correlations are improving data imputation performances, as well as labeling accuracy in real-world multi-label prediction tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge