Building robust classifiers through generation of confident out of distribution examples

Deep learning models are known to be overconfident in their predictions on out of distribution inputs. There have been several pieces of work to address this issue, including a number of approaches for building Bayesian neural networks, as well as closely related work on detection of out of distribution samples. Recently, there has been work on building classifiers that are robust to out of distribution samples by adding a regularization term that maximizes the entropy of the classifier output on out of distribution data. To approximate out of distribution samples (which are not known apriori), a GAN was used for generation of samples at the edges of the training distribution. In this paper, we introduce an alternative GAN based approach for building a robust classifier, where the idea is to use the GAN to explicitly generate out of distribution samples that the classifier is confident on (low entropy), and have the classifier maximize the entropy for these samples. We showcase the effectiveness of our approach relative to state-of-the-art on hand-written characters as well as on a variety of natural image datasets.

Improving robustness of classifiers by training against live traffic

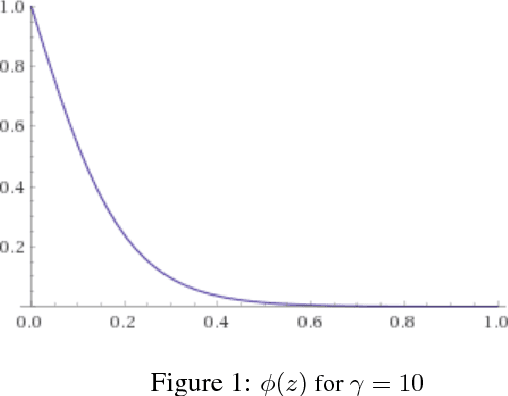
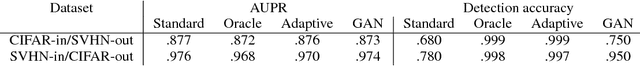
Deep learning models are known to be overconfident in their predictions on out of distribution inputs. This is a challenge when a model is trained on a particular input dataset, but receives out of sample data when deployed in practice. Recently, there has been work on building classifiers that are robust to out of distribution samples by adding a regularization term that maximizes the entropy of the classifier output on out of distribution data. However, given the challenge that it is not always possible to obtain out of distribution samples, the authors suggest a GAN based alternative that is independent of specific knowledge of out of distribution samples. From this existing work, we also know that having access to the true out of sample distribution for regularization works significantly better than using samples from the GAN. In this paper, we make the following observation: in practice, the out of distribution samples are contained in the traffic that hits a deployed classifier. However, the traffic will also contain a unknown proportion of in-distribution samples. If the entropy over of all of the traffic data were to be naively maximized, this will hurt the classifier performance on in-distribution data. To effectively leverage this traffic data, we propose an adaptive regularization technique (based on the maximum predictive probability score of a sample) which penalizes out of distribution samples more heavily than in distribution samples in the incoming traffic. This ensures that the overall performance of the classifier does not degrade on in-distribution data, while detection of out-of-distribution samples is significantly improved by leveraging the unlabeled traffic data. We show the effectiveness of our method via experiments on natural image datasets.

Latent Laplacian Maximum Entropy Discrimination for Detection of High-Utility Anomalies

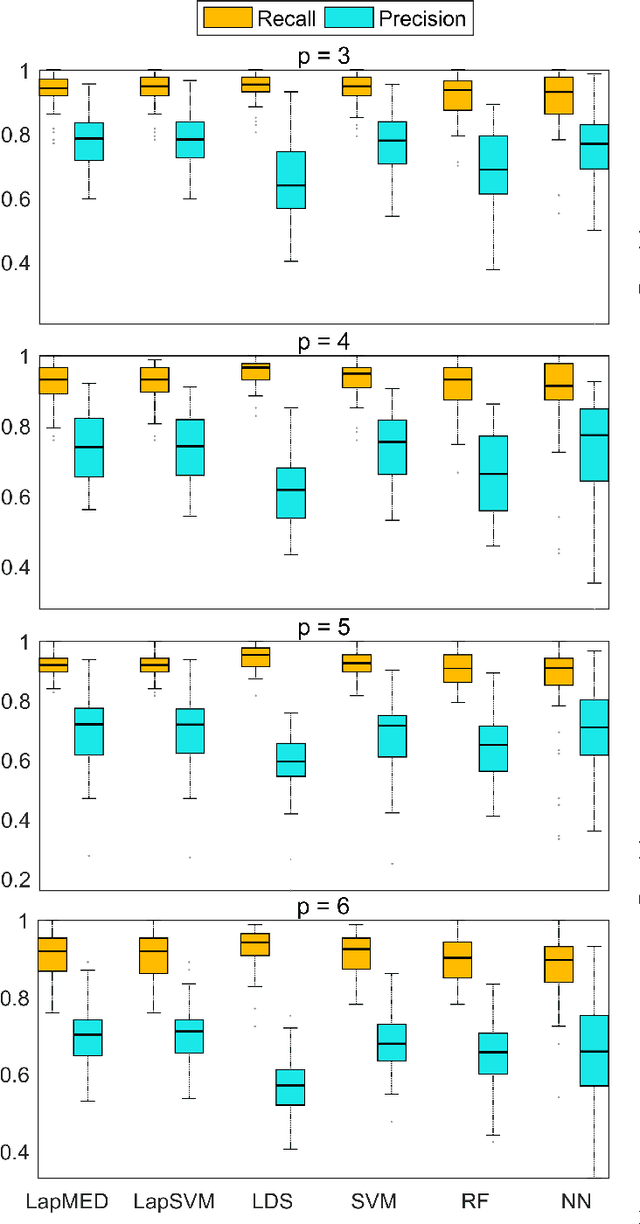
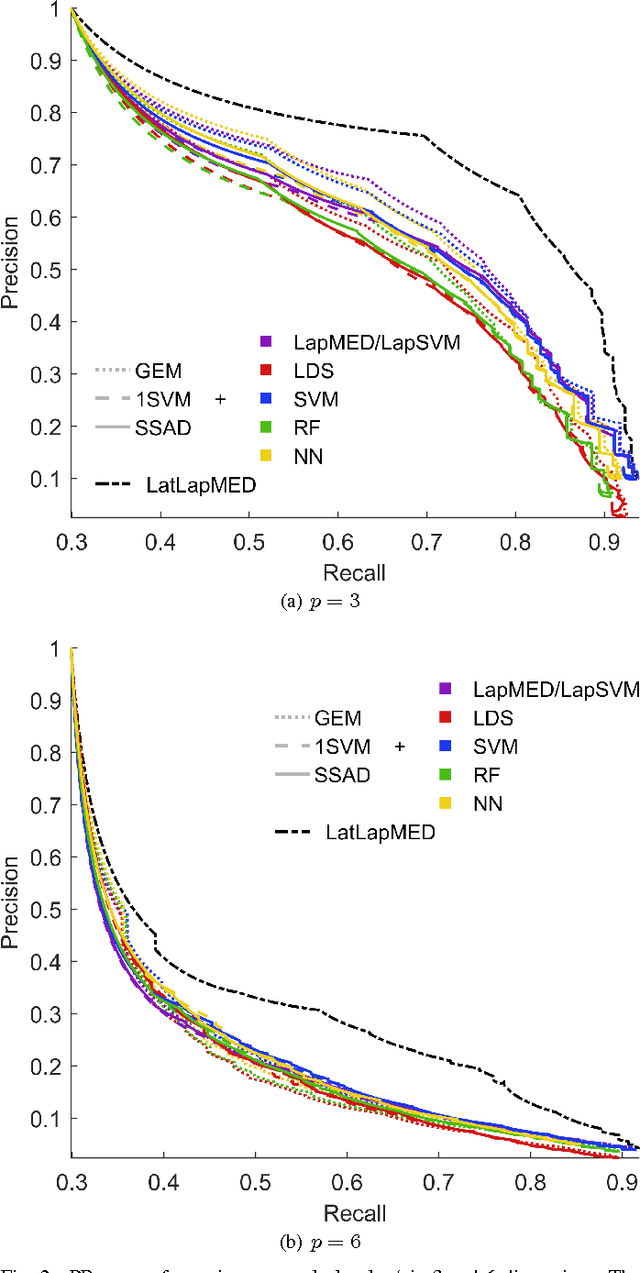
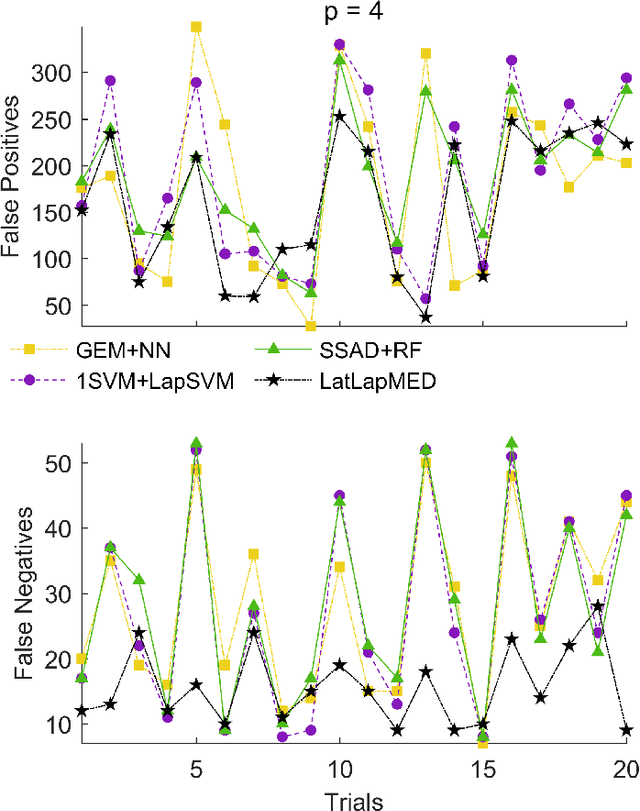
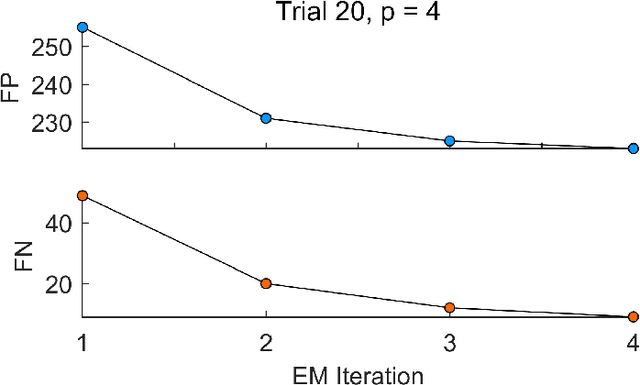
Data-driven anomaly detection methods suffer from the drawback of detecting all instances that are statistically rare, irrespective of whether the detected instances have real-world significance or not. In this paper, we are interested in the problem of specifically detecting anomalous instances that are known to have high real-world utility, while ignoring the low-utility statistically anomalous instances. To this end, we propose a novel method called Latent Laplacian Maximum Entropy Discrimination (LatLapMED) as a potential solution. This method uses the EM algorithm to simultaneously incorporate the Geometric Entropy Minimization principle for identifying statistical anomalies, and the Maximum Entropy Discrimination principle to incorporate utility labels, in order to detect high-utility anomalies. We apply our method in both simulated and real datasets to demonstrate that it has superior performance over existing alternatives that independently pre-process with unsupervised anomaly detection algorithms before classifying.

Recognizing Abnormal Heart Sounds Using Deep Learning

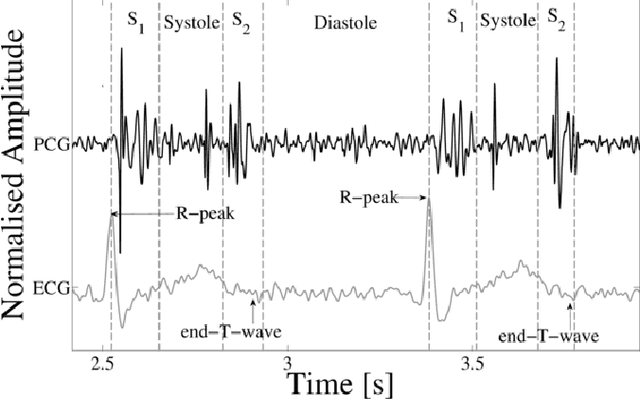
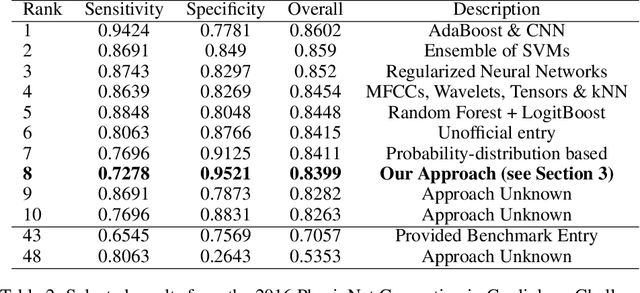
The work presented here applies deep learning to the task of automated cardiac auscultation, i.e. recognizing abnormalities in heart sounds. We describe an automated heart sound classification algorithm that combines the use of time-frequency heat map representations with a deep convolutional neural network (CNN). Given the cost-sensitive nature of misclassification, our CNN architecture is trained using a modified loss function that directly optimizes the trade-off between sensitivity and specificity. We evaluated our algorithm at the 2016 PhysioNet Computing in Cardiology challenge where the objective was to accurately classify normal and abnormal heart sounds from single, short, potentially noisy recordings. Our entry to the challenge achieved a final specificity of 0.95, sensitivity of 0.73 and overall score of 0.84. We achieved the greatest specificity score out of all challenge entries and, using just a single CNN, our algorithm differed in overall score by only 0.02 compared to the top place finisher, which used an ensemble approach.

ExprGAN: Facial Expression Editing with Controllable Expression Intensity

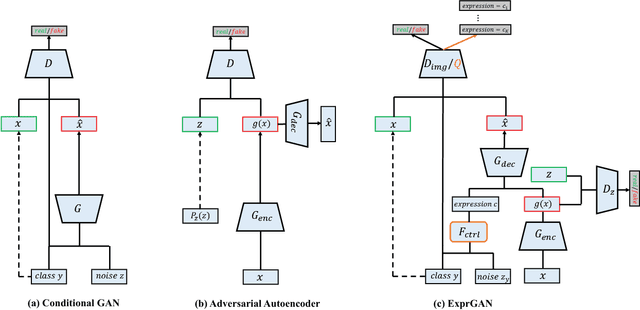
Facial expression editing is a challenging task as it needs a high-level semantic understanding of the input face image. In conventional methods, either paired training data is required or the synthetic face resolution is low. Moreover, only the categories of facial expression can be changed. To address these limitations, we propose an Expression Generative Adversarial Network (ExprGAN) for photo-realistic facial expression editing with controllable expression intensity. An expression controller module is specially designed to learn an expressive and compact expression code in addition to the encoder-decoder network. This novel architecture enables the expression intensity to be continuously adjusted from low to high. We further show that our ExprGAN can be applied for other tasks, such as expression transfer, image retrieval, and data augmentation for training improved face expression recognition models. To tackle the small size of the training database, an effective incremental learning scheme is proposed. Quantitative and qualitative evaluations on the widely used Oulu-CASIA dataset demonstrate the effectiveness of ExprGAN.

Semi-supervised Conditional GANs

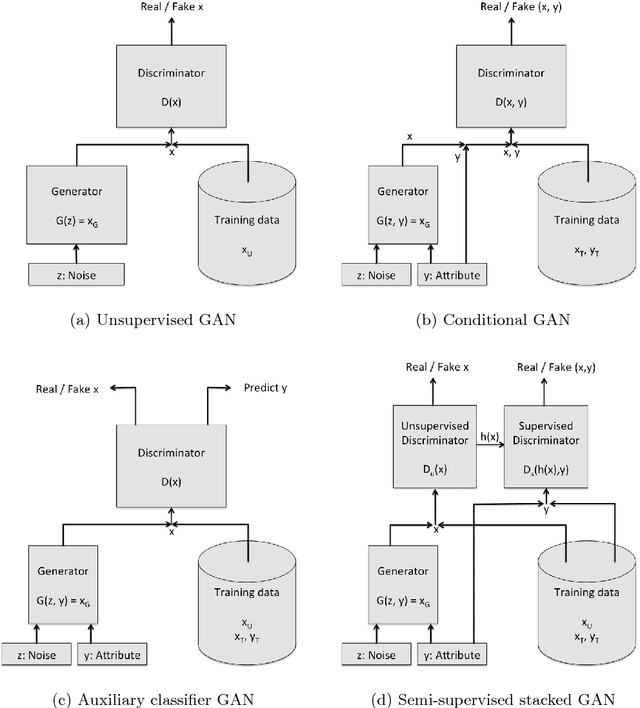
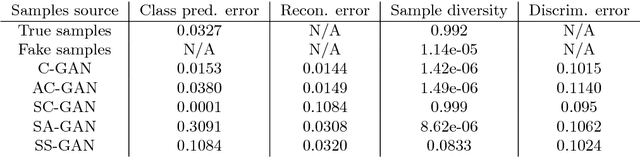
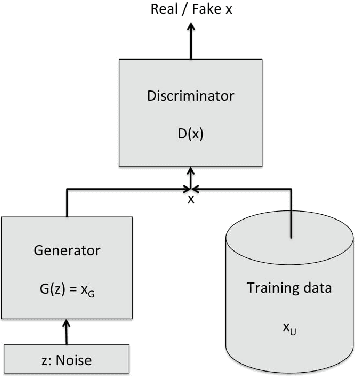
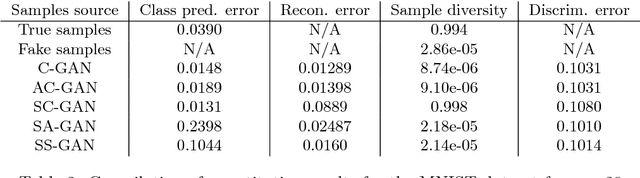
We introduce a new model for building conditional generative models in a semi-supervised setting to conditionally generate data given attributes by adapting the GAN framework. The proposed semi-supervised GAN (SS-GAN) model uses a pair of stacked discriminators to learn the marginal distribution of the data, and the conditional distribution of the attributes given the data respectively. In the semi-supervised setting, the marginal distribution (which is often harder to learn) is learned from the labeled + unlabeled data, and the conditional distribution is learned purely from the labeled data. Our experimental results demonstrate that this model performs significantly better compared to existing semi-supervised conditional GAN models.

Empirical estimation of entropy functionals with confidence

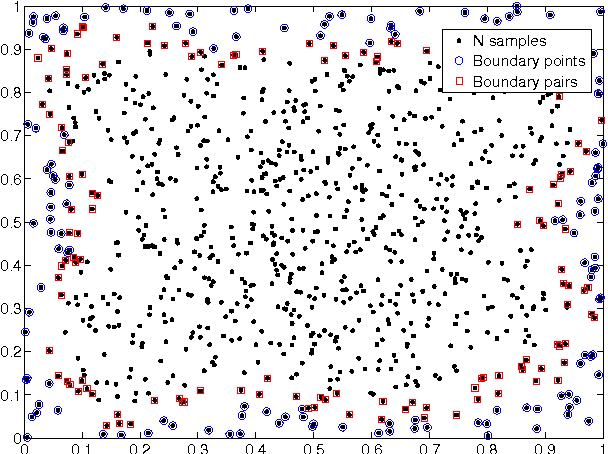
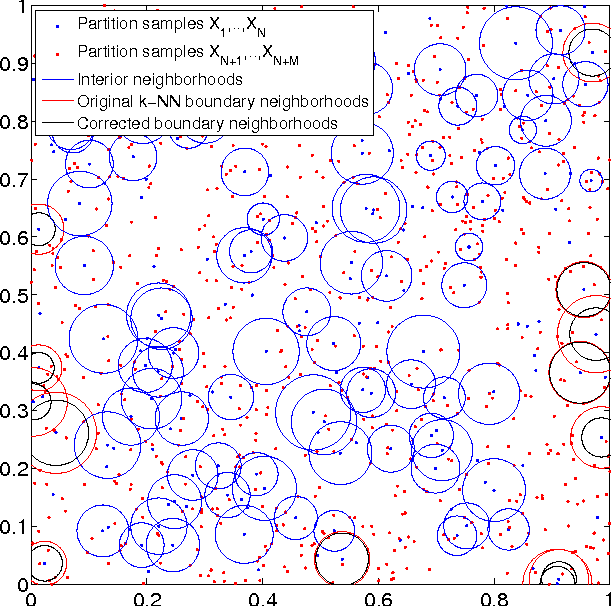
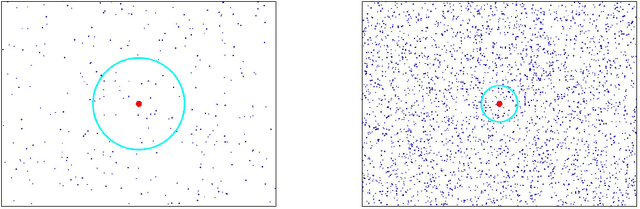
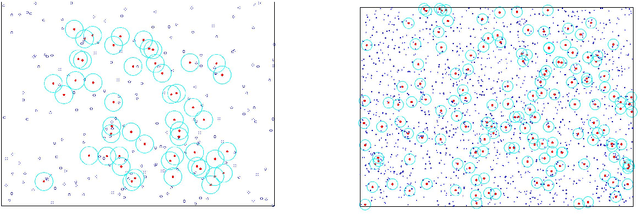
This paper introduces a class of k-nearest neighbor ($k$-NN) estimators called bipartite plug-in (BPI) estimators for estimating integrals of non-linear functions of a probability density, such as Shannon entropy and R\'enyi entropy. The density is assumed to be smooth, have bounded support, and be uniformly bounded from below on this set. Unlike previous $k$-NN estimators of non-linear density functionals, the proposed estimator uses data-splitting and boundary correction to achieve lower mean square error. Specifically, we assume that $T$ i.i.d. samples ${X}_i \in \mathbb{R}^d$ from the density are split into two pieces of cardinality $M$ and $N$ respectively, with $M$ samples used for computing a k-nearest-neighbor density estimate and the remaining $N$ samples used for empirical estimation of the integral of the density functional. By studying the statistical properties of k-NN balls, explicit rates for the bias and variance of the BPI estimator are derived in terms of the sample size, the dimension of the samples and the underlying probability distribution. Based on these results, it is possible to specify optimal choice of tuning parameters $M/T$, $k$ for maximizing the rate of decrease of the mean square error (MSE). The resultant optimized BPI estimator converges faster and achieves lower mean squared error than previous $k$-NN entropy estimators. In addition, a central limit theorem is established for the BPI estimator that allows us to specify tight asymptotic confidence intervals.