AI Enhanced Control Engineering Methods

AI and machine learning based approaches are becoming ubiquitous in almost all engineering fields. Control engineering cannot escape this trend. In this paper, we explore how AI tools can be useful in control applications. The core tool we focus on is automatic differentiation. Two immediate applications are linearization of system dynamics for local stability analysis or for state estimation using Kalman filters. We also explore other usages such as conversion of differential algebraic equations to ordinary differential equations for control design. In addition, we explore the use of machine learning models for global parameterizations of state vectors and control inputs in model predictive control applications. For each considered use case, we give examples and results.

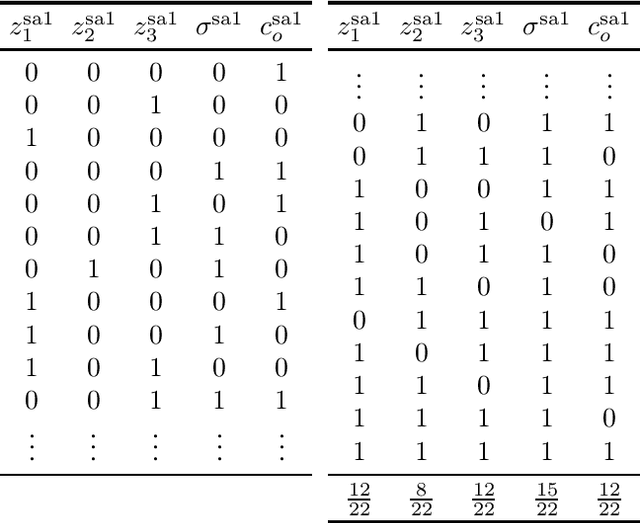
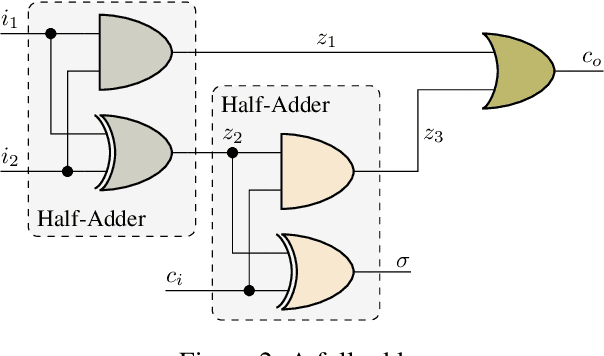
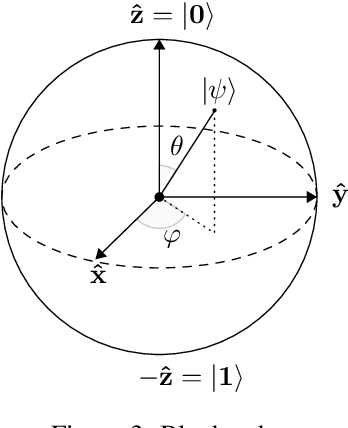
A Quantum Algorithm for Computing All Diagnoses of a Switching Circuit

Faults are stochastic by nature while most man-made systems, and especially computers, work deterministically. This necessitates the linking of probability theory with mathematical logics, automata, and switching circuit theory. This paper provides such a connecting via quantum information theory which is an intuitive approach as quantum physics obeys probability laws. In this paper we provide a novel approach for computing diagnosis of switching circuits with gate-based quantum computers. The approach is based on the idea of putting the qubits representing faults in superposition and compute all, often exponentially many, diagnoses simultaneously. We empirically compare the quantum algorithm for diagnostics to an approach based on SAT and model-counting. For a benchmark of combinational circuits we establish an error of less than one percent in estimating the true probability of faults.

System Resilience through Health Monitoring and Reconfiguration

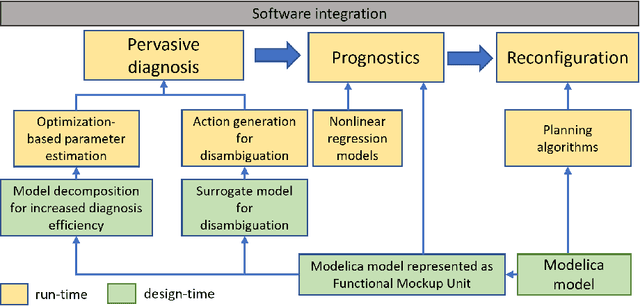
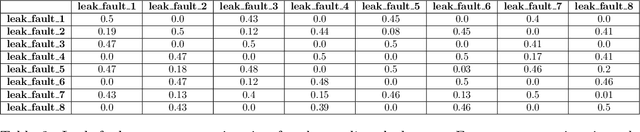
We demonstrate an end-to-end framework to improve the resilience of man-made systems to unforeseen events. The framework is based on a physics-based digital twin model and three modules tasked with real-time fault diagnosis, prognostics and reconfiguration. The fault diagnosis module uses model-based diagnosis algorithms to detect and isolate faults and generates interventions in the system to disambiguate uncertain diagnosis solutions. We scale up the fault diagnosis algorithm to the required real-time performance through the use of parallelization and surrogate models of the physics-based digital twin. The prognostics module tracks the fault progressions and trains the online degradation models to compute remaining useful life of system components. In addition, we use the degradation models to assess the impact of the fault progression on the operational requirements. The reconfiguration module uses PDDL-based planning endowed with semantic attachments to adjust the system controls so that the fault impact on the system operation is minimized. We define a resilience metric and use the example of a fuel system model to demonstrate how the metric improves with our framework.

Improving the Efficiency of Gradient Descent Algorithms Applied to Optimization Problems with Dynamical Constraints

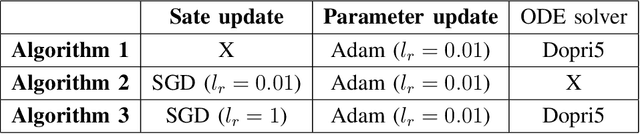
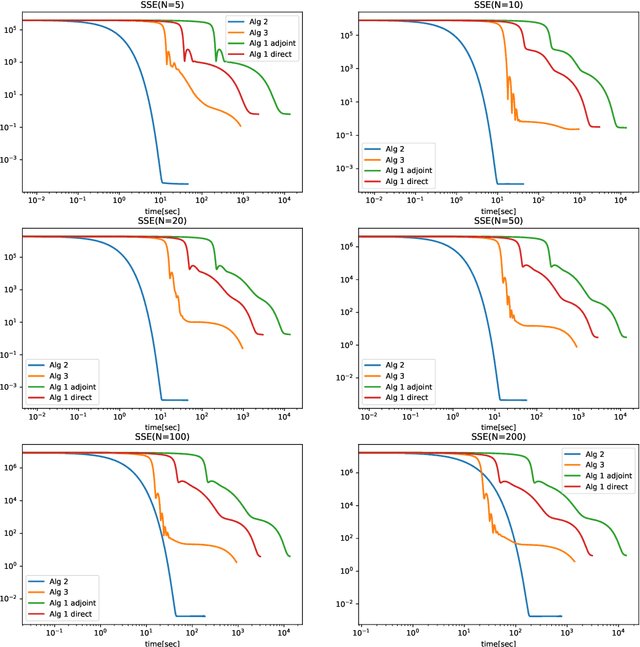
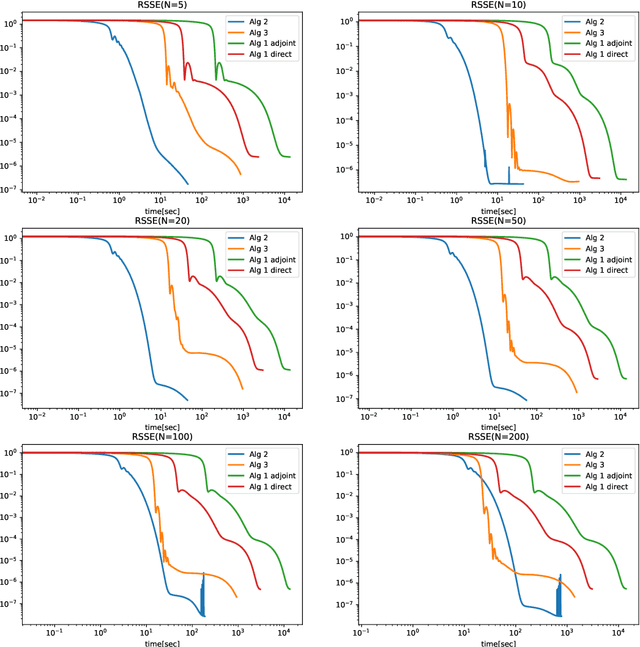
We introduce two block coordinate descent algorithms for solving optimization problems with ordinary differential equations (ODEs) as dynamical constraints. The algorithms do not need to implement direct or adjoint sensitivity analysis methods to evaluate loss function gradients. They results from reformulation of the original problem as an equivalent optimization problem with equality constraints. The algorithms naturally follow from steps aimed at recovering the gradient-decent algorithm based on ODE solvers that explicitly account for sensitivity of the ODE solution. In our first proposed algorithm we avoid explicitly solving the ODE by integrating the ODE solver as a sequence of implicit constraints. In our second algorithm, we use an ODE solver to reset the ODE solution, but no direct are adjoint sensitivity analysis methods are used. Both algorithm accepts mini-batch implementations and show significant efficiency benefits from GPU-based parallelization. We demonstrate the performance of the algorithms when applied to learning the parameters of the Cucker-Smale model. The algorithms are compared with gradient descent algorithms based on ODE solvers endowed with sensitivity analysis capabilities, for various number of state size, using Pytorch and Jax implementations. The experimental results demonstrate that the proposed algorithms are at least 4x faster than the Pytorch implementations, and at least 16x faster than Jax implementations. For large versions of the Cucker-Smale model, the Jax implementation is thousands of times faster than the sensitivity analysis-based implementation. In addition, our algorithms generate more accurate results both on training and test data. Such gains in computational efficiency is paramount for algorithms that implement real time parameter estimations, such as diagnosis algorithms.

Interpretable machine learning models: a physics-based view

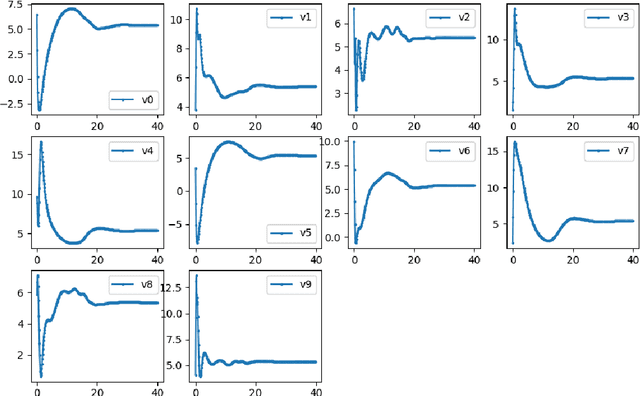
To understand changes in physical systems and facilitate decisions, explaining how model predictions are made is crucial. We use model-based interpretability, where models of physical systems are constructed by composing basic constructs that explain locally how energy is exchanged and transformed. We use the port Hamiltonian (p-H) formalism to describe the basic constructs that contain physically interpretable processes commonly found in the behavior of physical systems. We describe how we can build models out of the p-H constructs and how we can train them. In addition we show how we can impose physical properties such as dissipativity that ensure numerical stability of the training process. We give examples on how to build and train models for describing the behavior of two physical systems: the inverted pendulum and swarm dynamics.

Hybrid modeling: Applications in real-time diagnosis

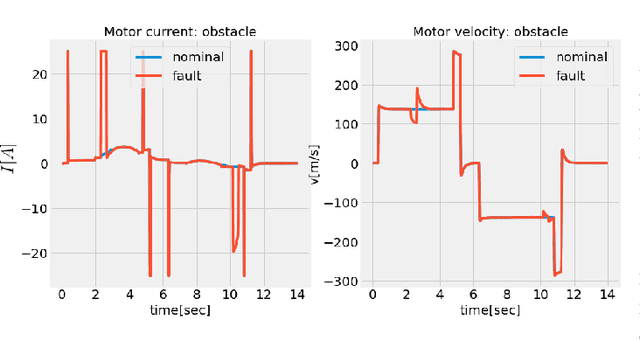
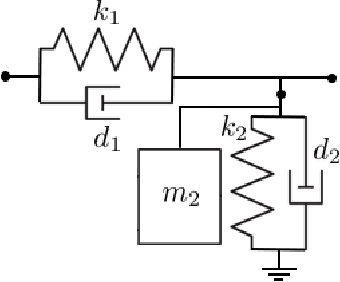
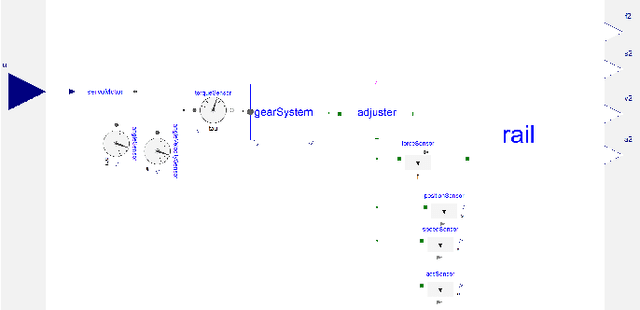
Reduced-order models that accurately abstract high fidelity models and enable faster simulation is vital for real-time, model-based diagnosis applications. In this paper, we outline a novel hybrid modeling approach that combines machine learning inspired models and physics-based models to generate reduced-order models from high fidelity models. We are using such models for real-time diagnosis applications. Specifically, we have developed machine learning inspired representations to generate reduced order component models that preserve, in part, the physical interpretation of the original high fidelity component models. To ensure the accuracy, scalability and numerical stability of the learning algorithms when training the reduced-order models we use optimization platforms featuring automatic differentiation. Training data is generated by simulating the high-fidelity model. We showcase our approach in the context of fault diagnosis of a rail switch system. Three new model abstractions whose complexities are two orders of magnitude smaller than the complexity of the high fidelity model, both in the number of equations and simulation time are shown. The numerical experiments and results demonstrate the efficacy of the proposed hybrid modeling approach.

Design Space Exploration as Quantified Satisfaction

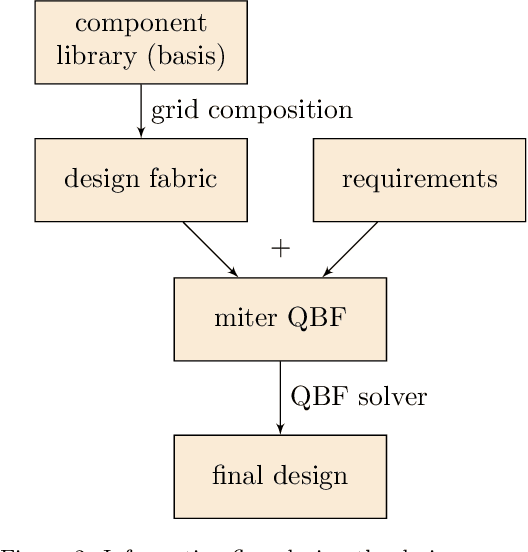
We propose novel algorithms for design and design space exploration. The designs computed by these algorithms are compositions of function types specified in component libraries. Our algorithms reduce the design problem to quantified satisfiability and use advanced solvers to find solutions that represent useful systems. The algorithms we present in this paper are sound and complete and are guaranteed to discover correct designs of optimal size, if they exist. We apply our method to the design of Boolean systems and discover new and more optimal classical and quantum circuits for common arithmetic functions such as addition and multiplication. The performance of our algorithms is evaluated through extensive experimentation. We have first created a benchmark consisting of specifications of scalable synthetic digital circuits and real-world mirochips. We have then generated multiple circuits functionally equivalent to the ones in the benchmark. The quantified satisfiability method shows more than four orders of magnitude speed-up, compared to a generate and test method that enumerates all non-isomorphic circuit topologies. Our approach generalizes circuit optimization. It uses arbitrary component libraries and has applications to areas such as digital circuit design, diagnostics, abductive reasoning, test vector generation, and combinatorial optimization.

Recognizing Abnormal Heart Sounds Using Deep Learning

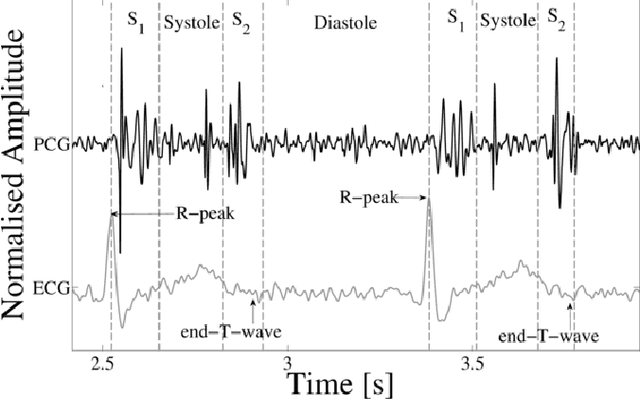
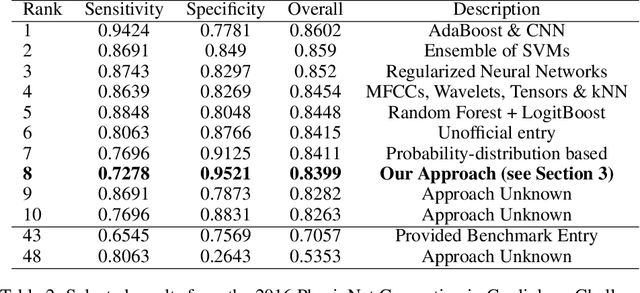
The work presented here applies deep learning to the task of automated cardiac auscultation, i.e. recognizing abnormalities in heart sounds. We describe an automated heart sound classification algorithm that combines the use of time-frequency heat map representations with a deep convolutional neural network (CNN). Given the cost-sensitive nature of misclassification, our CNN architecture is trained using a modified loss function that directly optimizes the trade-off between sensitivity and specificity. We evaluated our algorithm at the 2016 PhysioNet Computing in Cardiology challenge where the objective was to accurately classify normal and abnormal heart sounds from single, short, potentially noisy recordings. Our entry to the challenge achieved a final specificity of 0.95, sensitivity of 0.73 and overall score of 0.84. We achieved the greatest specificity score out of all challenge entries and, using just a single CNN, our algorithm differed in overall score by only 0.02 compared to the top place finisher, which used an ensemble approach.