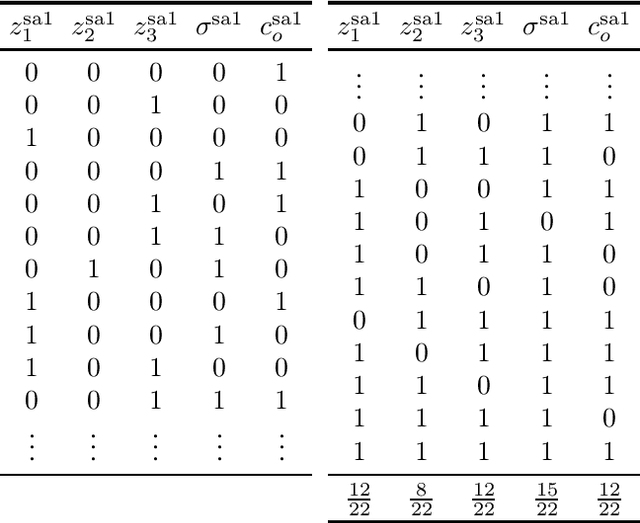
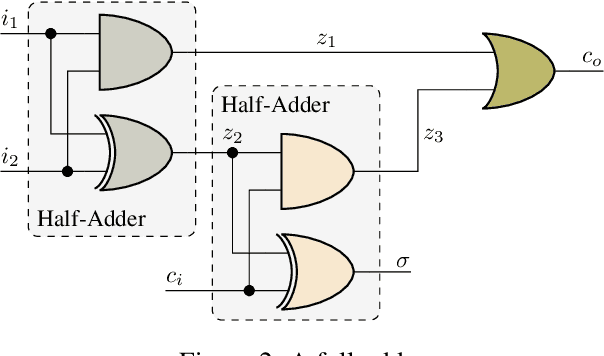
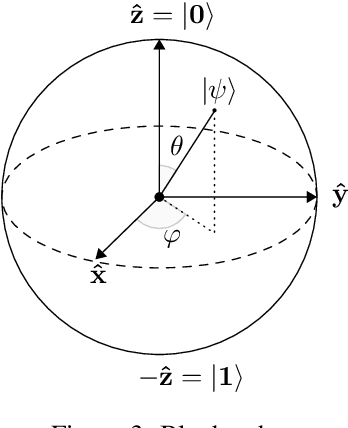
A Quantum Algorithm for Computing All Diagnoses of a Switching Circuit

Faults are stochastic by nature while most man-made systems, and especially computers, work deterministically. This necessitates the linking of probability theory with mathematical logics, automata, and switching circuit theory. This paper provides such a connecting via quantum information theory which is an intuitive approach as quantum physics obeys probability laws. In this paper we provide a novel approach for computing diagnosis of switching circuits with gate-based quantum computers. The approach is based on the idea of putting the qubits representing faults in superposition and compute all, often exponentially many, diagnoses simultaneously. We empirically compare the quantum algorithm for diagnostics to an approach based on SAT and model-counting. For a benchmark of combinational circuits we establish an error of less than one percent in estimating the true probability of faults.

Hybrid modeling: Applications in real-time diagnosis

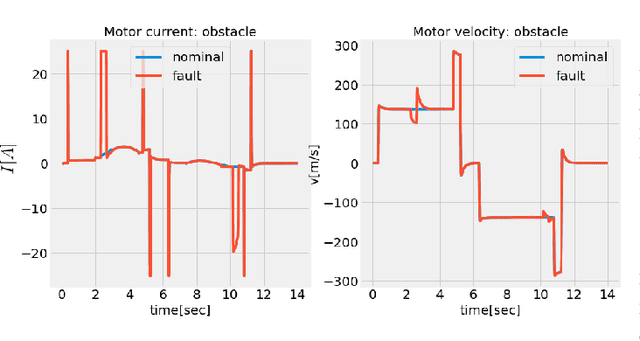
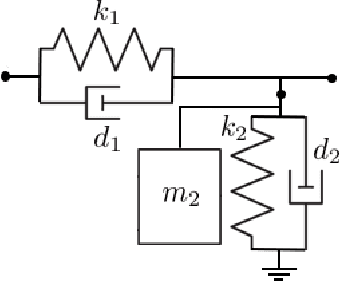
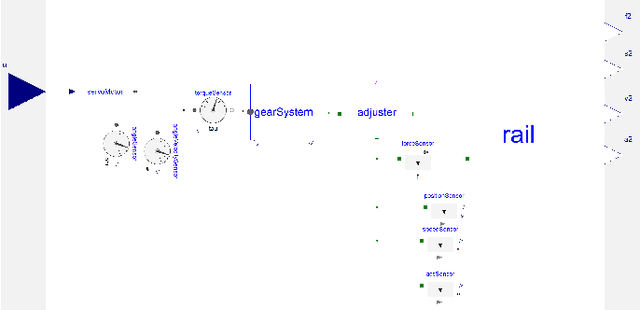
Reduced-order models that accurately abstract high fidelity models and enable faster simulation is vital for real-time, model-based diagnosis applications. In this paper, we outline a novel hybrid modeling approach that combines machine learning inspired models and physics-based models to generate reduced-order models from high fidelity models. We are using such models for real-time diagnosis applications. Specifically, we have developed machine learning inspired representations to generate reduced order component models that preserve, in part, the physical interpretation of the original high fidelity component models. To ensure the accuracy, scalability and numerical stability of the learning algorithms when training the reduced-order models we use optimization platforms featuring automatic differentiation. Training data is generated by simulating the high-fidelity model. We showcase our approach in the context of fault diagnosis of a rail switch system. Three new model abstractions whose complexities are two orders of magnitude smaller than the complexity of the high fidelity model, both in the number of equations and simulation time are shown. The numerical experiments and results demonstrate the efficacy of the proposed hybrid modeling approach.

Design Space Exploration as Quantified Satisfaction

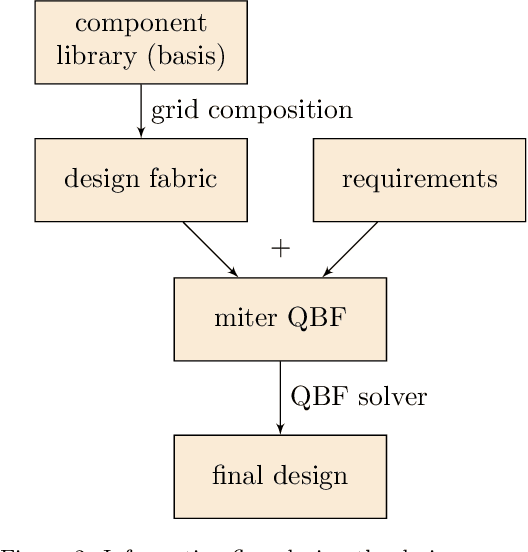
We propose novel algorithms for design and design space exploration. The designs computed by these algorithms are compositions of function types specified in component libraries. Our algorithms reduce the design problem to quantified satisfiability and use advanced solvers to find solutions that represent useful systems. The algorithms we present in this paper are sound and complete and are guaranteed to discover correct designs of optimal size, if they exist. We apply our method to the design of Boolean systems and discover new and more optimal classical and quantum circuits for common arithmetic functions such as addition and multiplication. The performance of our algorithms is evaluated through extensive experimentation. We have first created a benchmark consisting of specifications of scalable synthetic digital circuits and real-world mirochips. We have then generated multiple circuits functionally equivalent to the ones in the benchmark. The quantified satisfiability method shows more than four orders of magnitude speed-up, compared to a generate and test method that enumerates all non-isomorphic circuit topologies. Our approach generalizes circuit optimization. It uses arbitrary component libraries and has applications to areas such as digital circuit design, diagnostics, abductive reasoning, test vector generation, and combinatorial optimization.

A Model-Based Active Testing Approach to Sequential Diagnosis

Model-based diagnostic reasoning often leads to a large number of diagnostic hypotheses. The set of diagnoses can be reduced by taking into account extra observations (passive monitoring), measuring additional variables (probing) or executing additional tests (sequential diagnosis/test sequencing). In this paper we combine the above approaches with techniques from Automated Test Pattern Generation (ATPG) and Model-Based Diagnosis (MBD) into a framework called FRACTAL (FRamework for ACtive Testing ALgorithms). Apart from the inputs and outputs that connect a system to its environment, in active testing we consider additional input variables to which a sequence of test vectors can be supplied. We address the computationally hard problem of computing optimal control assignments (as defined in FRACTAL) in terms of a greedy approximation algorithm called FRACTAL-G. We compare the decrease in the number of remaining minimal cardinality diagnoses of FRACTAL-G to that of two more FRACTAL algorithms: FRACTAL-ATPG and FRACTAL-P. FRACTAL-ATPG is based on ATPG and sequential diagnosis while FRACTAL-P is based on probing and, although not an active testing algorithm, provides a baseline for comparing the lower bound on the number of reachable diagnoses for the FRACTAL algorithms. We empirically evaluate the trade-offs of the three FRACTAL algorithms by performing extensive experimentation on the ISCAS85/74XXX benchmark of combinational circuits.

Approximate Model-Based Diagnosis Using Greedy Stochastic Search

We propose a StochAstic Fault diagnosis AlgoRIthm, called SAFARI, which trades off guarantees of computing minimal diagnoses for computational efficiency. We empirically demonstrate, using the 74XXX and ISCAS-85 suites of benchmark combinatorial circuits, that SAFARI achieves several orders-of-magnitude speedup over two well-known deterministic algorithms, CDA* and HA*, for multiple-fault diagnoses; further, SAFARI can compute a range of multiple-fault diagnoses that CDA* and HA* cannot. We also prove that SAFARI is optimal for a range of propositional fault models, such as the widely-used weak-fault models (models with ignorance of abnormal behavior). We discuss the optimality of SAFARI in a class of strong-fault circuit models with stuck-at failure modes. By modeling the algorithm itself as a Markov chain, we provide exact bounds on the minimality of the diagnosis computed. SAFARI also displays strong anytime behavior, and will return a diagnosis after any non-trivial inference time.