Design Space Exploration as Quantified Satisfaction

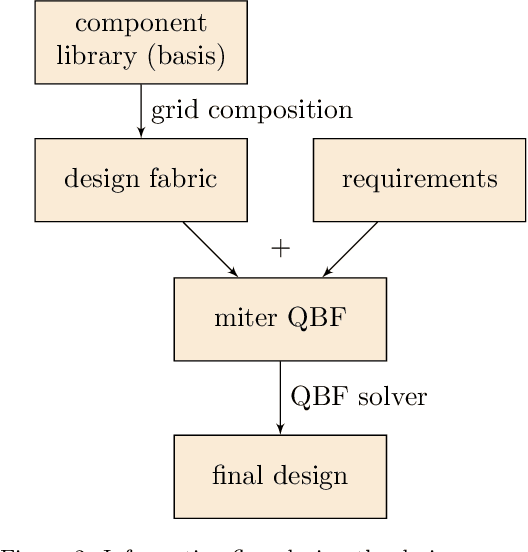
We propose novel algorithms for design and design space exploration. The designs computed by these algorithms are compositions of function types specified in component libraries. Our algorithms reduce the design problem to quantified satisfiability and use advanced solvers to find solutions that represent useful systems. The algorithms we present in this paper are sound and complete and are guaranteed to discover correct designs of optimal size, if they exist. We apply our method to the design of Boolean systems and discover new and more optimal classical and quantum circuits for common arithmetic functions such as addition and multiplication. The performance of our algorithms is evaluated through extensive experimentation. We have first created a benchmark consisting of specifications of scalable synthetic digital circuits and real-world mirochips. We have then generated multiple circuits functionally equivalent to the ones in the benchmark. The quantified satisfiability method shows more than four orders of magnitude speed-up, compared to a generate and test method that enumerates all non-isomorphic circuit topologies. Our approach generalizes circuit optimization. It uses arbitrary component libraries and has applications to areas such as digital circuit design, diagnostics, abductive reasoning, test vector generation, and combinatorial optimization.