On Local Linear Convergence of Projected Gradient Descent for Unit-Modulus Least Squares
Paper and Code
Jul 01, 2022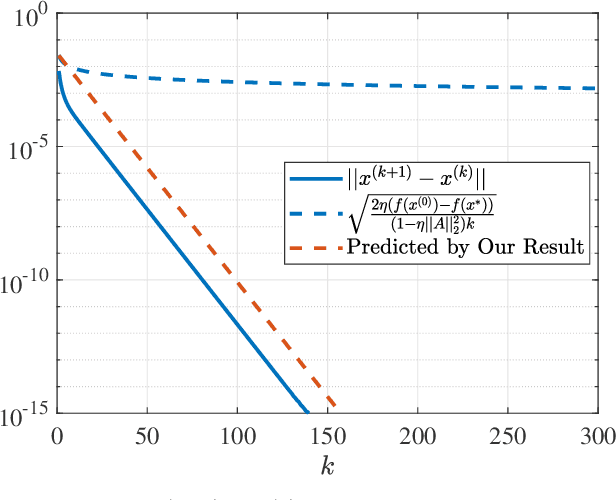
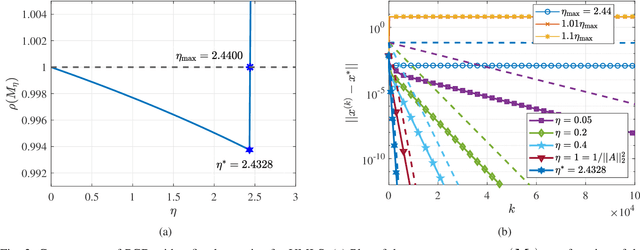
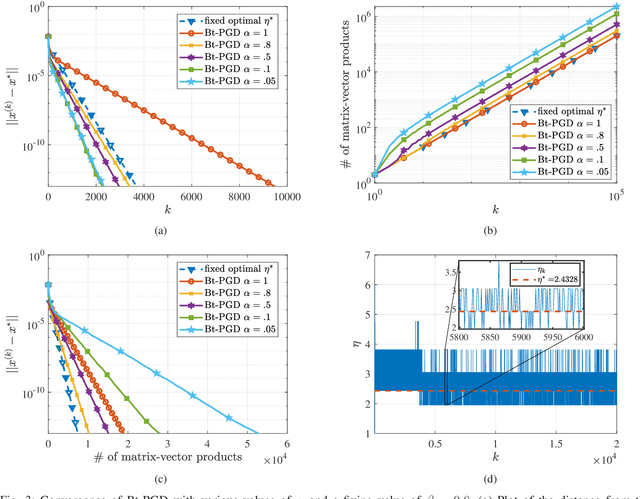
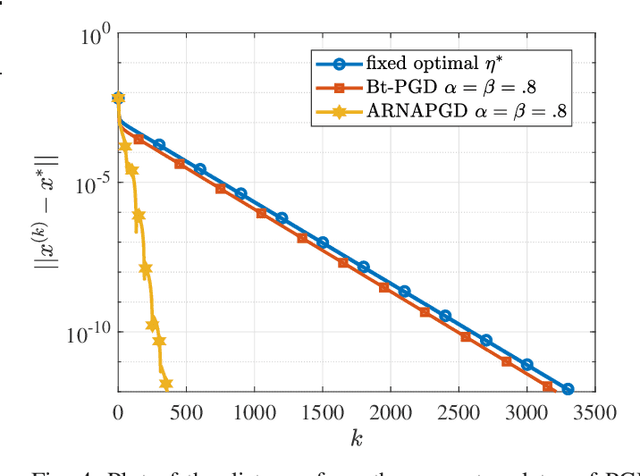
The unit-modulus least squares (UMLS) problem has a wide spectrum of applications in signal processing, e.g., phase-only beamforming, phase retrieval, radar code design, and sensor network localization. Scalable first-order methods such as projected gradient descent (PGD) have recently been studied as a simple yet efficient approach to solving the UMLS problem. Existing results on the convergence of PGD for UMLS often focus on global convergence to stationary points. As a non-convex problem, only a sublinear convergence rate has been established. However, these results do not explain the fast convergence of PGD frequently observed in practice. This manuscript presents a novel analysis of convergence of PGD for UMLS, justifying the linear convergence behavior of the algorithm near the solution. By exploiting the local structure of the objective function and the constraint set, we establish an exact expression for the convergence rate and characterize the conditions for linear convergence. Simulations show that our theoretical analysis corroborates numerical examples. Furthermore, variants of PGD with adaptive step sizes are proposed based on the new insight revealed in our convergence analysis. The variants show substantial acceleration in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge