Parkinson's Disease Digital Biomarker Discovery with Optimized Transitions and Inferred Markov Emissions
Paper and Code
Nov 11, 2017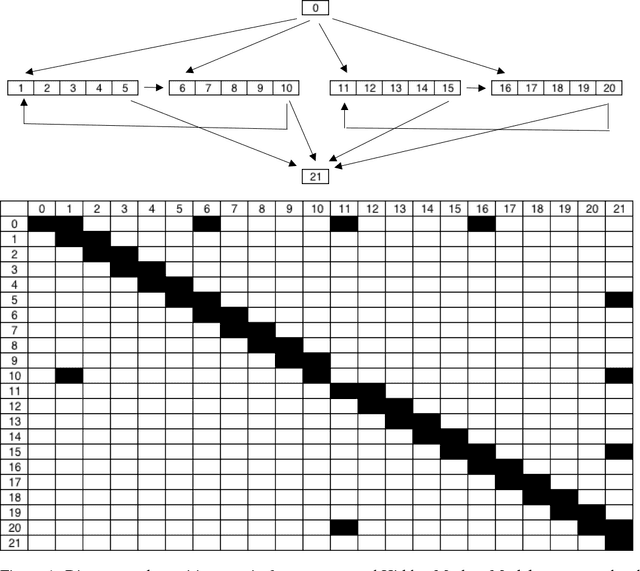
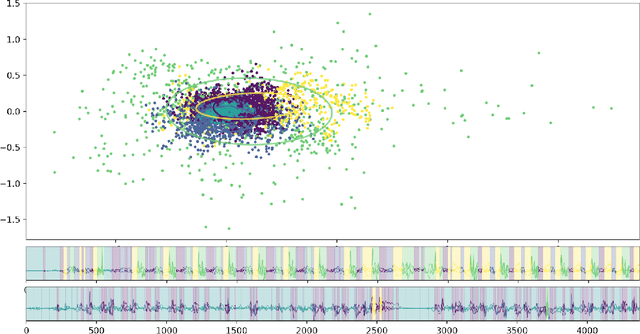
We search for digital biomarkers from Parkinson's Disease by observing approximate repetitive patterns matching hypothesized step and stride periodic cycles. These observations were modeled as a cycle of hidden states with randomness allowing deviation from a canonical pattern of transitions and emissions, under the hypothesis that the averaged features of hidden states would serve to informatively characterize classes of patients/controls. We propose a Hidden Semi-Markov Model (HSMM), a latent-state model, emitting 3D-acceleration vectors. Transitions and emissions are inferred from data. We fit separate models per unique device and training label. Hidden Markov Models (HMM) force geometric distributions of the duration spent at each state before transition to a new state. Instead, our HSMM allows us to specify the distribution of state duration. This modified version is more effective because we are interested more in each state's duration than the sequence of distinct states, allowing inclusion of these durations the feature vector.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge