Recommender Systems with Generative Retrieval

Modern recommender systems leverage large-scale retrieval models consisting of two stages: training a dual-encoder model to embed queries and candidates in the same space, followed by an Approximate Nearest Neighbor (ANN) search to select top candidates given a query's embedding. In this paper, we propose a new single-stage paradigm: a generative retrieval model which autoregressively decodes the identifiers for the target candidates in one phase. To do this, instead of assigning randomly generated atomic IDs to each item, we generate Semantic IDs: a semantically meaningful tuple of codewords for each item that serves as its unique identifier. We use a hierarchical method called RQ-VAE to generate these codewords. Once we have the Semantic IDs for all the items, a Transformer based sequence-to-sequence model is trained to predict the Semantic ID of the next item. Since this model predicts the tuple of codewords identifying the next item directly in an autoregressive manner, it can be considered a generative retrieval model. We show that our recommender system trained in this new paradigm improves the results achieved by current SOTA models on the Amazon dataset. Moreover, we demonstrate that the sequence-to-sequence model coupled with hierarchical Semantic IDs offers better generalization and hence improves retrieval of cold-start items for recommendations.

Matrix Completion from Noisy Entries

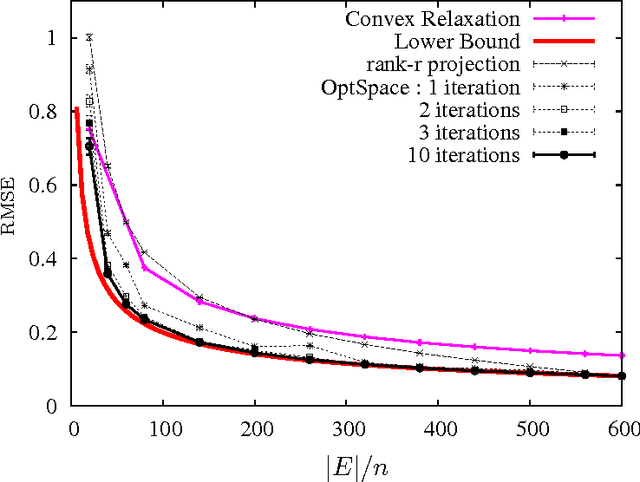
Given a matrix M of low-rank, we consider the problem of reconstructing it from noisy observations of a small, random subset of its entries. The problem arises in a variety of applications, from collaborative filtering (the `Netflix problem') to structure-from-motion and positioning. We study a low complexity algorithm introduced by Keshavan et al.(2009), based on a combination of spectral techniques and manifold optimization, that we call here OptSpace. We prove performance guarantees that are order-optimal in a number of circumstances.

Regularization for Matrix Completion

We consider the problem of reconstructing a low rank matrix from noisy observations of a subset of its entries. This task has applications in statistical learning, computer vision, and signal processing. In these contexts, "noise" generically refers to any contribution to the data that is not captured by the low-rank model. In most applications, the noise level is large compared to the underlying signal and it is important to avoid overfitting. In order to tackle this problem, we define a regularized cost function well suited for spectral reconstruction methods. Within a random noise model, and in the large system limit, we prove that the resulting accuracy undergoes a phase transition depending on the noise level and on the fraction of observed entries. The cost function can be minimized using OPTSPACE (a manifold gradient descent algorithm). Numerical simulations show that this approach is competitive with state-of-the-art alternatives.

Low-rank Matrix Completion with Noisy Observations: a Quantitative Comparison

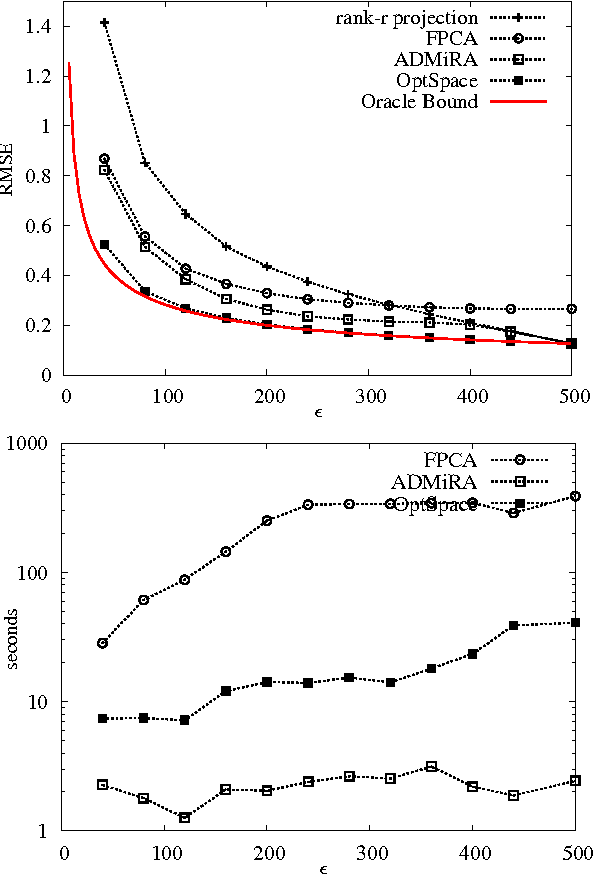
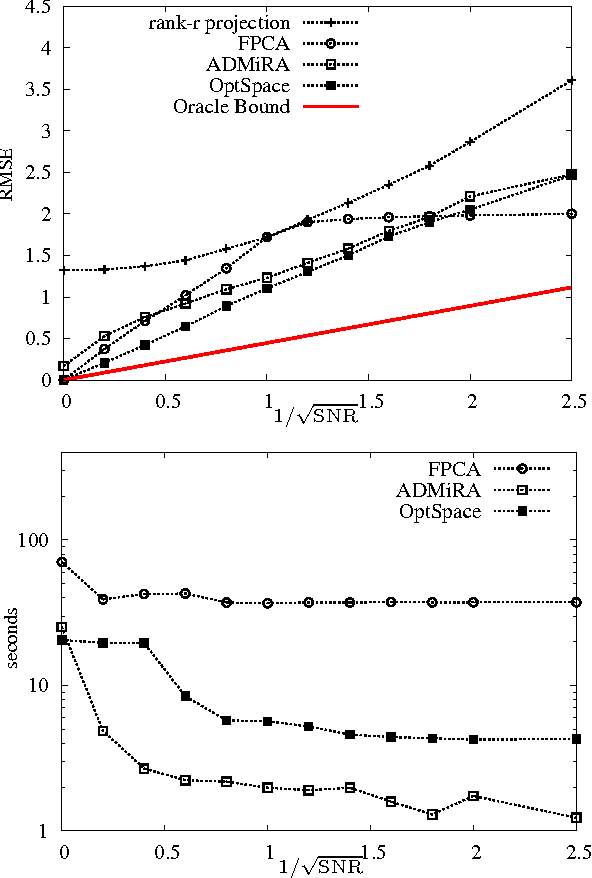
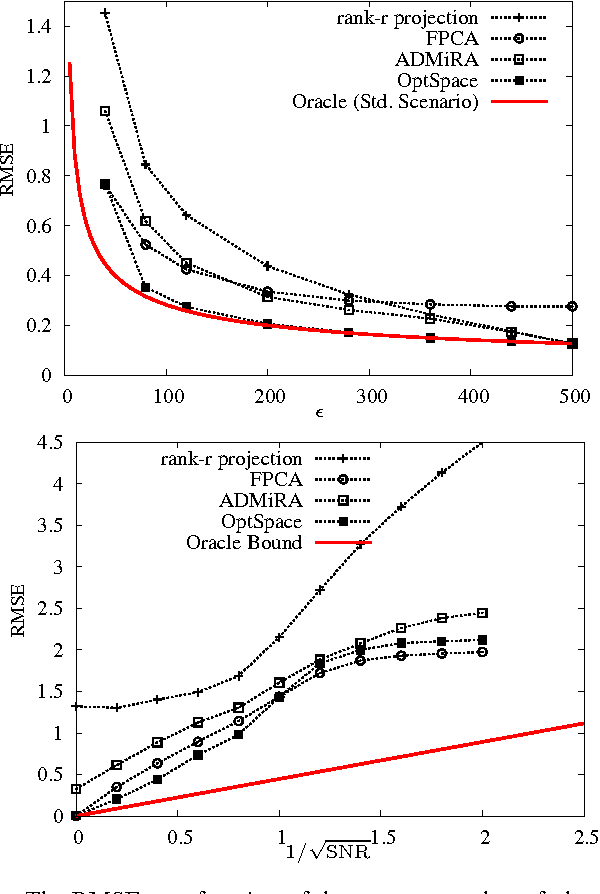
We consider a problem of significant practical importance, namely, the reconstruction of a low-rank data matrix from a small subset of its entries. This problem appears in many areas such as collaborative filtering, computer vision and wireless sensor networks. In this paper, we focus on the matrix completion problem in the case when the observed samples are corrupted by noise. We compare the performance of three state-of-the-art matrix completion algorithms (OptSpace, ADMiRA and FPCA) on a single simulation platform and present numerical results. We show that in practice these efficient algorithms can be used to reconstruct real data matrices, as well as randomly generated matrices, accurately.

A Gradient Descent Algorithm on the Grassman Manifold for Matrix Completion

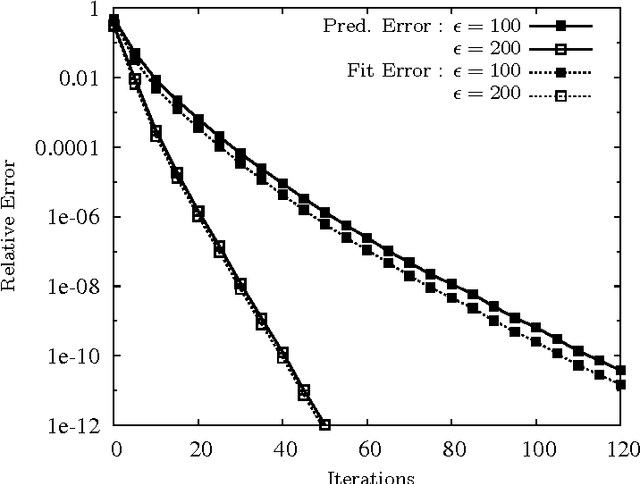
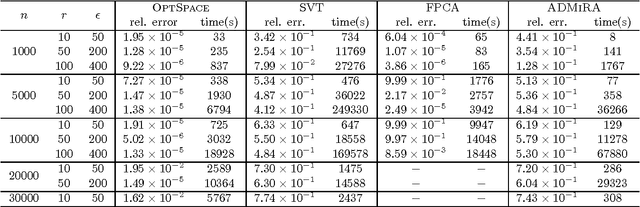
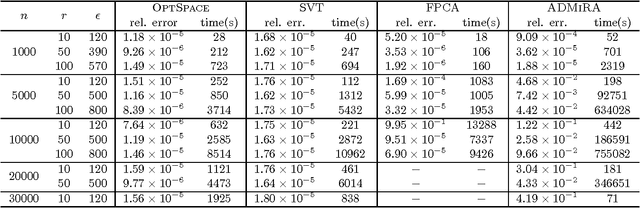
We consider the problem of reconstructing a low-rank matrix from a small subset of its entries. In this paper, we describe the implementation of an efficient algorithm called OptSpace, based on singular value decomposition followed by local manifold optimization, for solving the low-rank matrix completion problem. It has been shown that if the number of revealed entries is large enough, the output of singular value decomposition gives a good estimate for the original matrix, so that local optimization reconstructs the correct matrix with high probability. We present numerical results which show that this algorithm can reconstruct the low rank matrix exactly from a very small subset of its entries. We further study the robustness of the algorithm with respect to noise, and its performance on actual collaborative filtering datasets.

Matrix Completion from a Few Entries

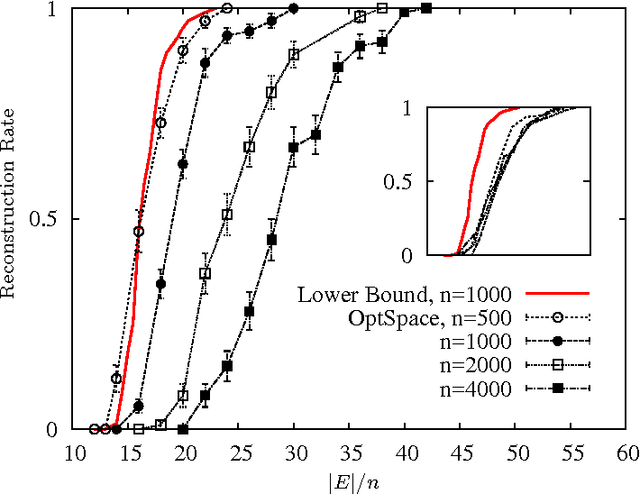
Let M be a random (alpha n) x n matrix of rank r<<n, and assume that a uniformly random subset E of its entries is observed. We describe an efficient algorithm that reconstructs M from |E| = O(rn) observed entries with relative root mean square error RMSE <= C(rn/|E|)^0.5 . Further, if r=O(1), M can be reconstructed exactly from |E| = O(n log(n)) entries. These results apply beyond random matrices to general low-rank incoherent matrices. This settles (in the case of bounded rank) a question left open by Candes and Recht and improves over the guarantees for their reconstruction algorithm. The complexity of our algorithm is O(|E|r log(n)), which opens the way to its use for massive data sets. In the process of proving these statements, we obtain a generalization of a celebrated result by Friedman-Kahn-Szemeredi and Feige-Ofek on the spectrum of sparse random matrices.