Matrix Completion from Noisy Entries
Paper and Code
Apr 09, 2012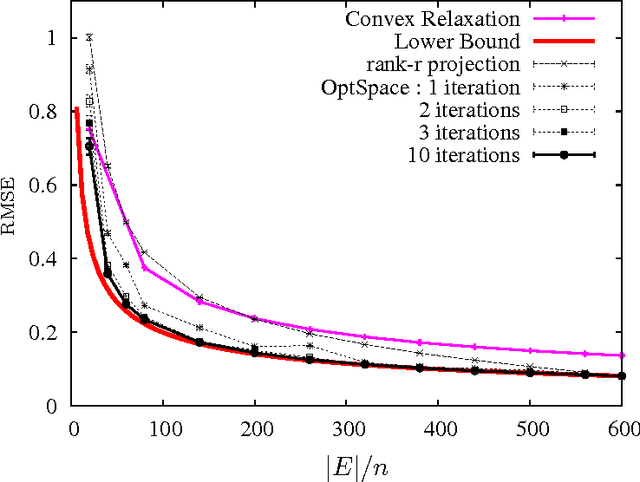
Given a matrix M of low-rank, we consider the problem of reconstructing it from noisy observations of a small, random subset of its entries. The problem arises in a variety of applications, from collaborative filtering (the `Netflix problem') to structure-from-motion and positioning. We study a low complexity algorithm introduced by Keshavan et al.(2009), based on a combination of spectral techniques and manifold optimization, that we call here OptSpace. We prove performance guarantees that are order-optimal in a number of circumstances.
* 22 pages, 3 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge