Low-rank Matrix Completion with Noisy Observations: a Quantitative Comparison

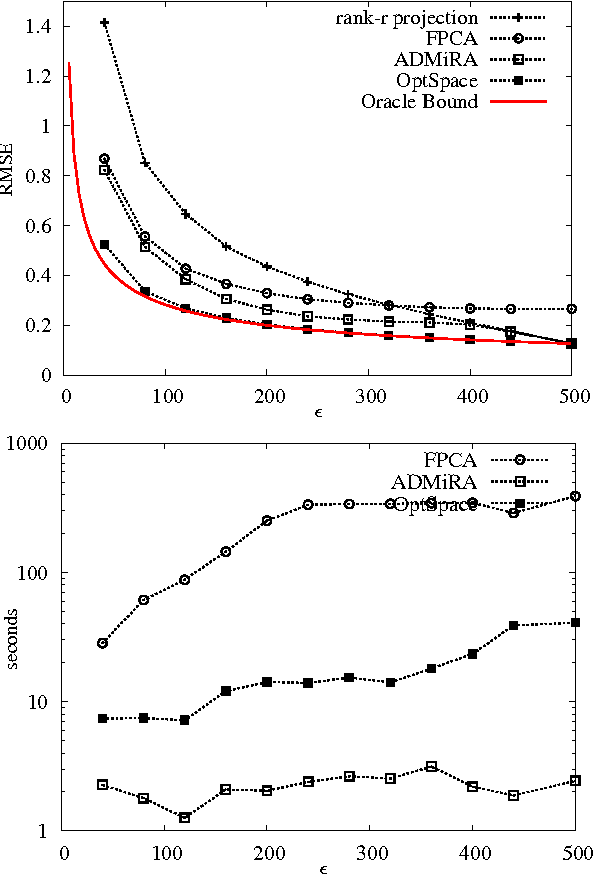
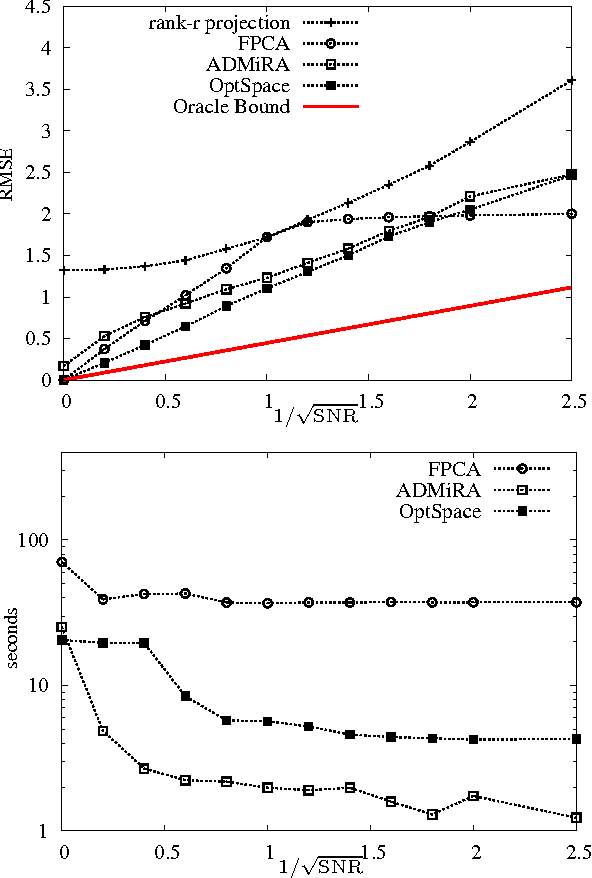
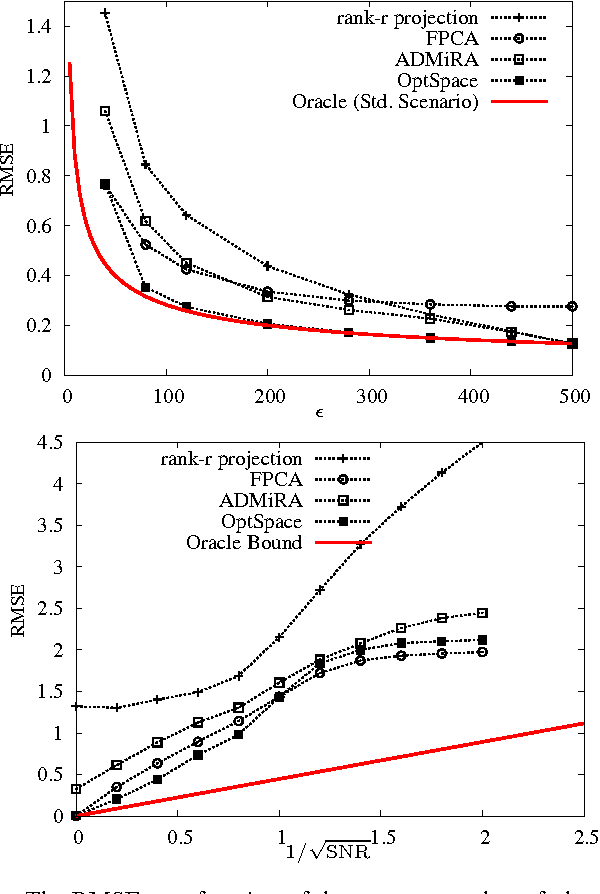
We consider a problem of significant practical importance, namely, the reconstruction of a low-rank data matrix from a small subset of its entries. This problem appears in many areas such as collaborative filtering, computer vision and wireless sensor networks. In this paper, we focus on the matrix completion problem in the case when the observed samples are corrupted by noise. We compare the performance of three state-of-the-art matrix completion algorithms (OptSpace, ADMiRA and FPCA) on a single simulation platform and present numerical results. We show that in practice these efficient algorithms can be used to reconstruct real data matrices, as well as randomly generated matrices, accurately.