Monotonicity in practice of adaptive testing

In our previous work we have shown how Bayesian networks can be used for adaptive testing of student skills. Later, we have taken the advantage of monotonicity restrictions in order to learn models fitting data better. This article provides a synergy between these two phases as it evaluates Bayesian network models used for computerized adaptive testing and learned with a recently proposed monotonicity gradient algorithm. This learning method is compared with another monotone method, the isotonic regression EM algorithm. The quality of methods is empirically evaluated on a large data set of the Czech National Mathematics Exam. Besides advantages of adaptive testing approach we observed also advantageous behavior of monotonic methods, especially for small learning data set sizes. Another novelty of this work is the use of the reliability interval of the score distribution, which is used to predict student's final score and grade. In the experiments we have clearly shown we can shorten the test while keeping its reliability. We have also shown that the monotonicity increases the prediction quality with limited training data sets. The monotone model learned by the gradient method has a lower question prediction quality than unrestricted models but it is better in the main target of this application, which is the student score prediction. It is an important observation that a mere optimization of the model likelihood or the prediction accuracy do not necessarily lead to a model that describes best the student.

Solving the Goddard problem by an influence diagram

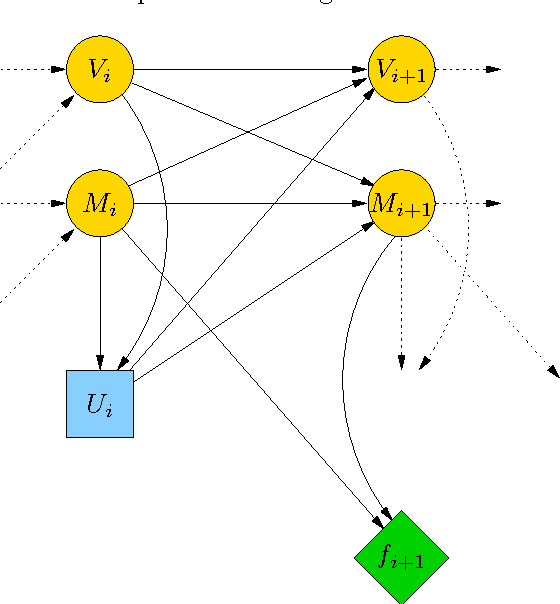
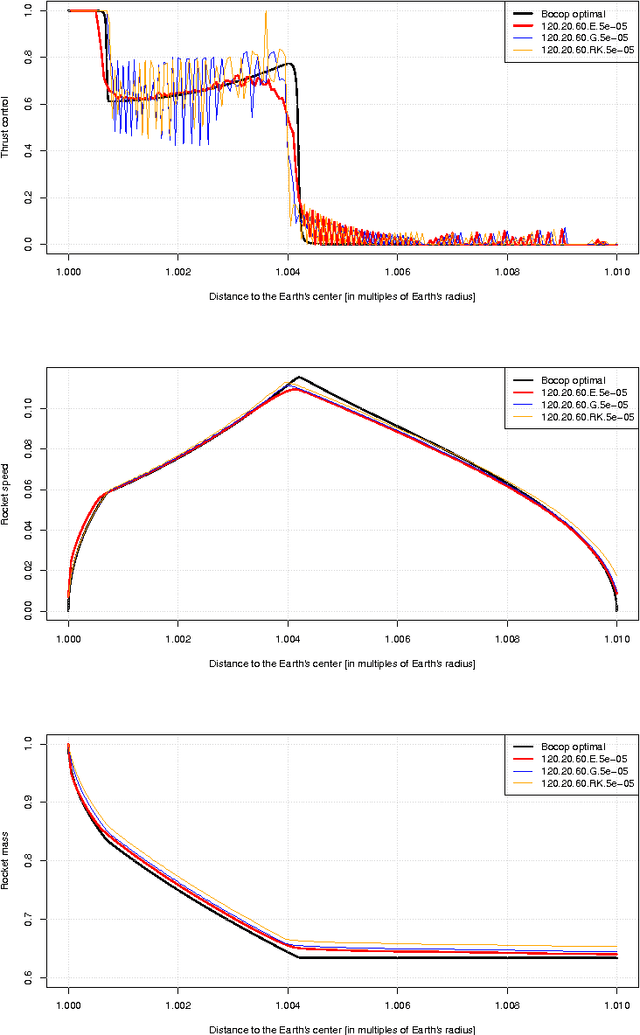
Influence diagrams are a decision-theoretic extension of probabilistic graphical models. In this paper we show how they can be used to solve the Goddard problem. We present results of numerical experiments with this problem and compare the solutions provided by influence diagrams with the optimal solution.

Solving the Brachistochrone Problem by an Influence Diagram

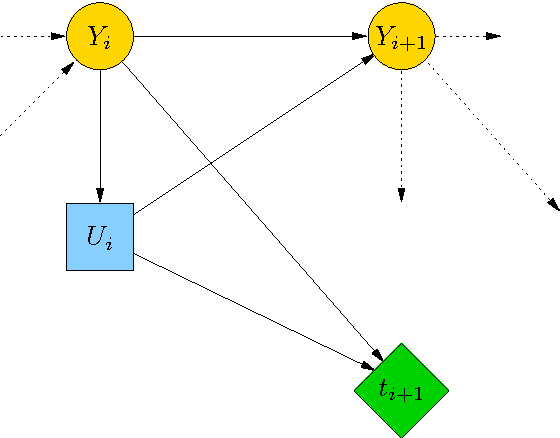
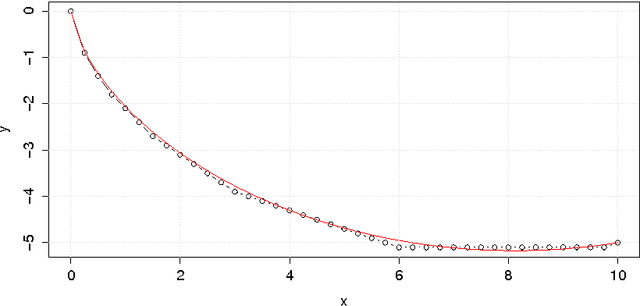
Influence diagrams are a decision-theoretic extension of probabilistic graphical models. In this paper we show how they can be used to solve the Brachistochrone problem. We present results of numerical experiments on this problem, compare the solution provided by the influence diagram with the optimal solution. The R code used for the experiments is presented in the Appendix.

Probabilistic Models for Computerized Adaptive Testing: Experiments

This paper follows previous research we have already performed in the area of Bayesian networks models for CAT. We present models using Item Response Theory (IRT - standard CAT method), Bayesian networks, and neural networks. We conducted simulated CAT tests on empirical data. Results of these tests are presented for each model separately and compared.

Influence diagrams for the optimization of a vehicle speed profile

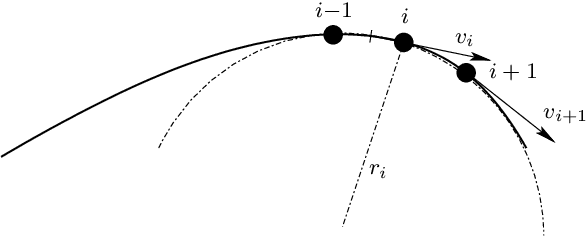
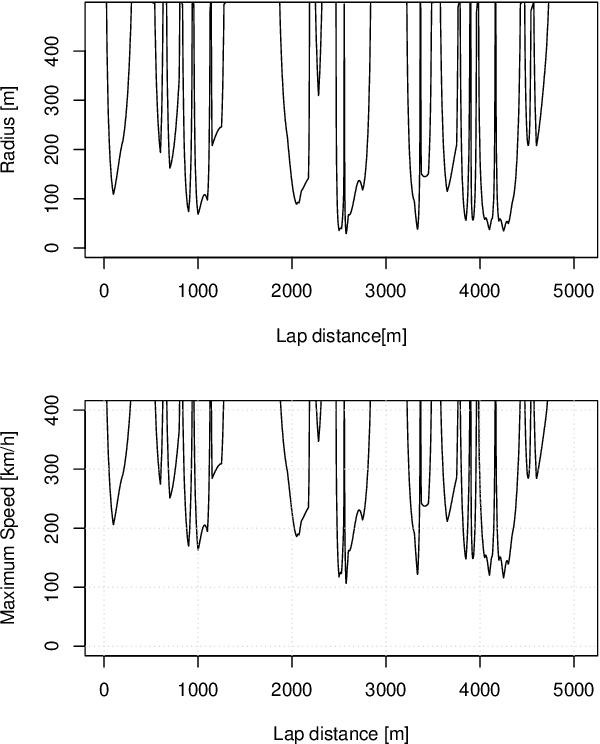
Influence diagrams are decision theoretic extensions of Bayesian networks. They are applied to diverse decision problems. In this paper we apply influence diagrams to the optimization of a vehicle speed profile. We present results of computational experiments in which an influence diagram was used to optimize the speed profile of a Formula 1 race car at the Silverstone F1 circuit. The computed lap time and speed profiles correspond well to those achieved by test pilots. An extended version of our model that considers a more complex optimization function and diverse traffic constraints is currently being tested onboard a testing car by a major car manufacturer. This paper opens doors for new applications of influence diagrams.

Bayesian Network Models for Adaptive Testing

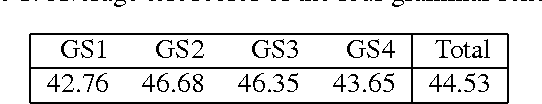
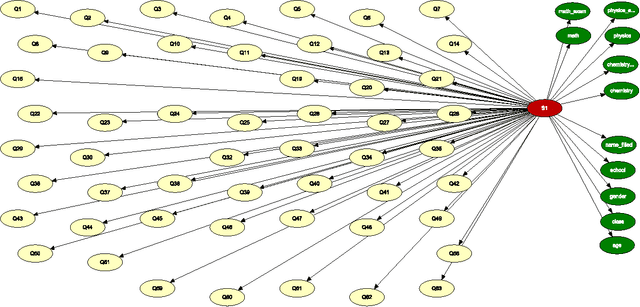
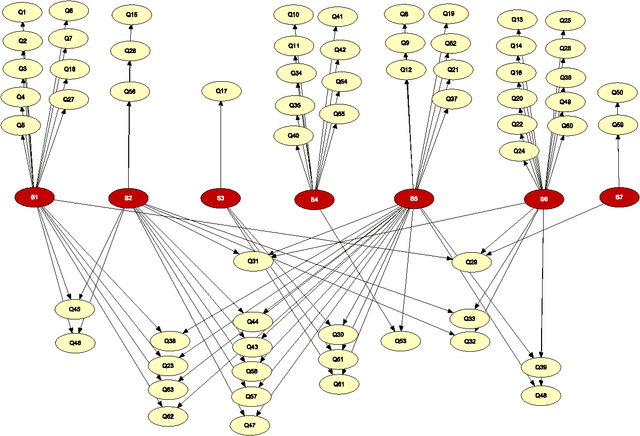
Computerized adaptive testing (CAT) is an interesting and promising approach to testing human abilities. In our research we use Bayesian networks to create a model of tested humans. We collected data from paper tests performed with grammar school students. In this article we first provide the summary of data used for our experiments. We propose several different Bayesian networks, which we tested and compared by cross-validation. Interesting results were obtained and are discussed in the paper. The analysis has brought a clearer view on the model selection problem. Future research is outlined in the concluding part of the paper.

On tensor rank of conditional probability tables in Bayesian networks

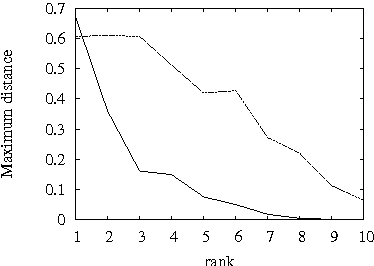
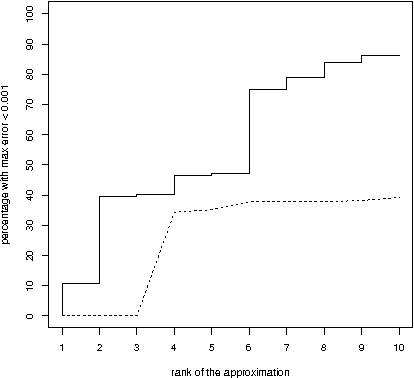
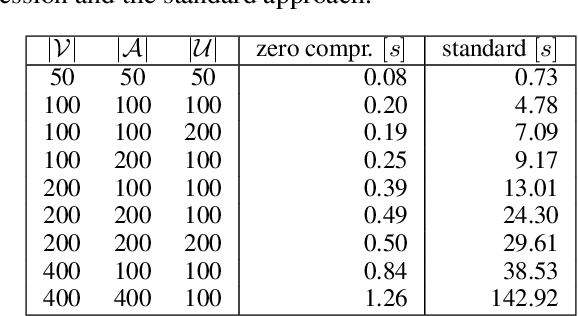
A difficult task in modeling with Bayesian networks is the elicitation of numerical parameters of Bayesian networks. A large number of parameters is needed to specify a conditional probability table (CPT) that has a larger parent set. In this paper we show that, most CPTs from real applications of Bayesian networks can actually be very well approximated by tables that require substantially less parameters. This observation has practical consequence not only for model elicitation but also for efficient probabilistic reasoning with these networks.