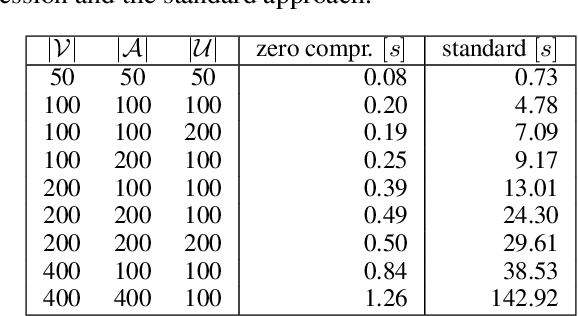
Composition of Credal Sets via Polyhedral Geometry

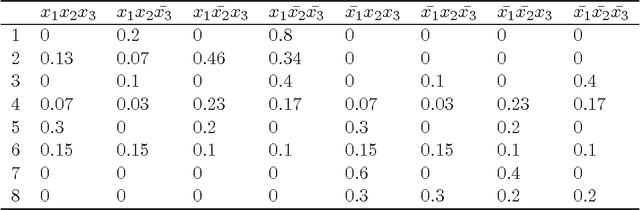
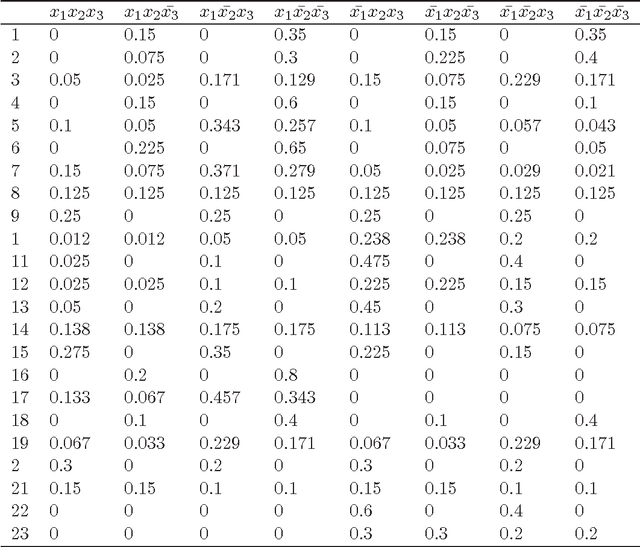
Recently introduced composition operator for credal sets is an analogy of such operators in probability, possibility, evidence and valuation-based systems theories. It was designed to construct multidimensional models (in the framework of credal sets) from a system of low- dimensional credal sets. In this paper we study its potential from the computational point of view utilizing methods of polyhedral geometry.

Solving the Goddard problem by an influence diagram

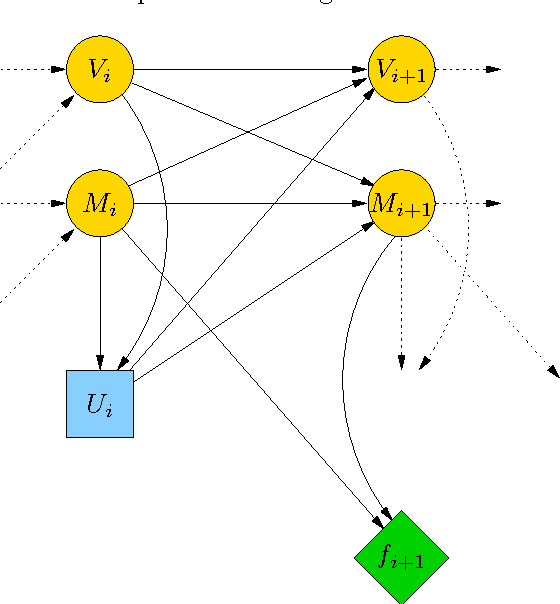
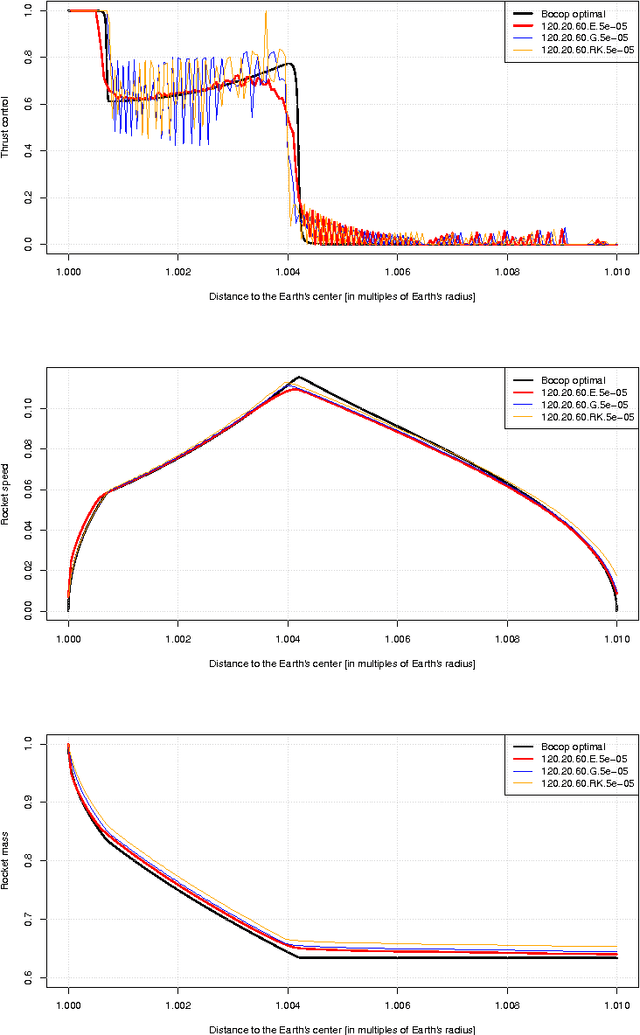
Influence diagrams are a decision-theoretic extension of probabilistic graphical models. In this paper we show how they can be used to solve the Goddard problem. We present results of numerical experiments with this problem and compare the solutions provided by influence diagrams with the optimal solution.

Influence diagrams for the optimization of a vehicle speed profile

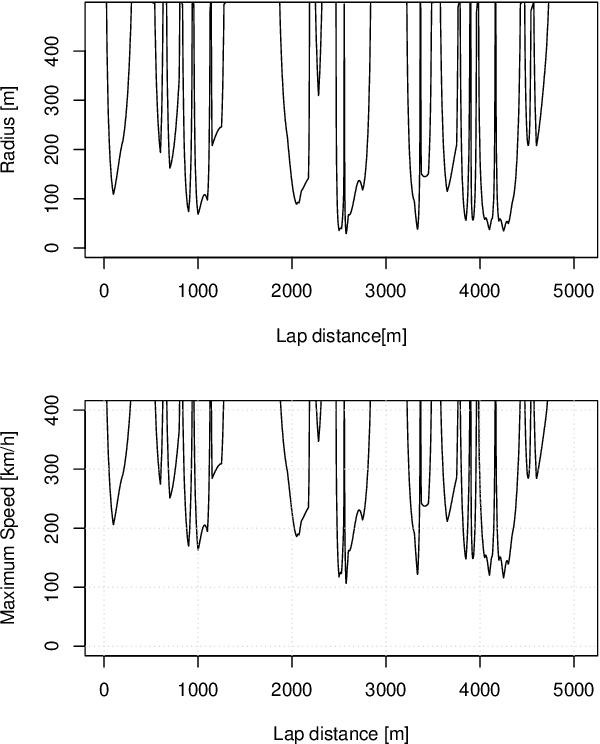
Influence diagrams are decision theoretic extensions of Bayesian networks. They are applied to diverse decision problems. In this paper we apply influence diagrams to the optimization of a vehicle speed profile. We present results of computational experiments in which an influence diagram was used to optimize the speed profile of a Formula 1 race car at the Silverstone F1 circuit. The computed lap time and speed profiles correspond well to those achieved by test pilots. An extended version of our model that considers a more complex optimization function and diverse traffic constraints is currently being tested onboard a testing car by a major car manufacturer. This paper opens doors for new applications of influence diagrams.