How to Train Unstable Looped Tensor Network

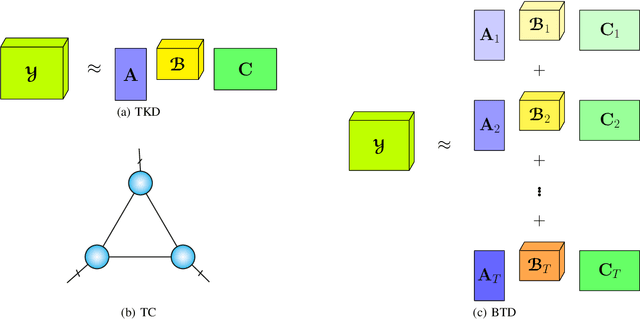
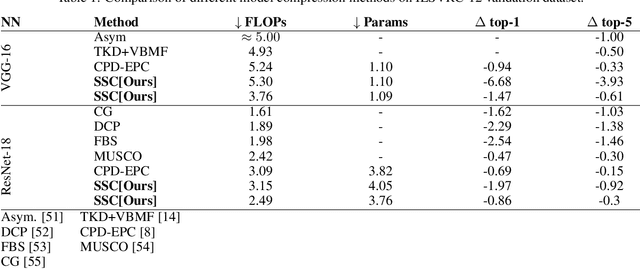
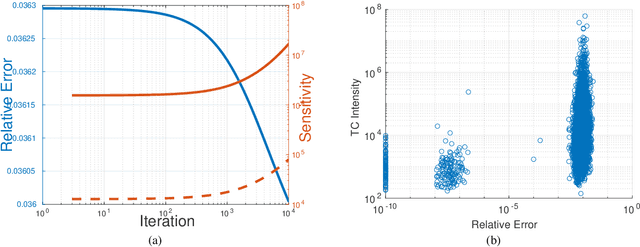
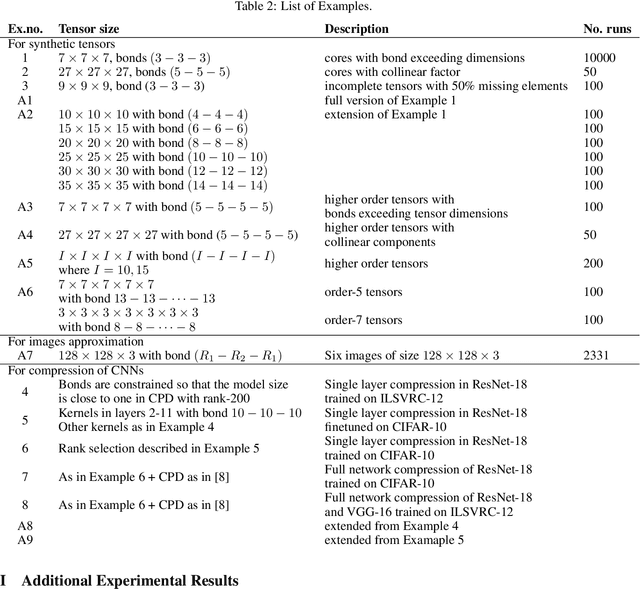
A rising problem in the compression of Deep Neural Networks is how to reduce the number of parameters in convolutional kernels and the complexity of these layers by low-rank tensor approximation. Canonical polyadic tensor decomposition (CPD) and Tucker tensor decomposition (TKD) are two solutions to this problem and provide promising results. However, CPD often fails due to degeneracy, making the networks unstable and hard to fine-tune. TKD does not provide much compression if the core tensor is big. This motivates using a hybrid model of CPD and TKD, a decomposition with multiple Tucker models with small core tensor, known as block term decomposition (BTD). This paper proposes a more compact model that further compresses the BTD by enforcing core tensors in BTD identical. We establish a link between the BTD with shared parameters and a looped chain tensor network (TC). Unfortunately, such strongly constrained tensor networks (with loop) encounter severe numerical instability, as proved by y (Landsberg, 2012) and (Handschuh, 2015a). We study perturbation of chain tensor networks, provide interpretation of instability in TC, demonstrate the problem. We propose novel methods to gain the stability of the decomposition results, keep the network robust and attain better approximation. Experimental results will confirm the superiority of the proposed methods in compression of well-known CNNs, and TC decomposition under challenging scenarios

CNN Acceleration by Low-rank Approximation with Quantized Factors

The modern convolutional neural networks although achieve great results in solving complex computer vision tasks still cannot be effectively used in mobile and embedded devices due to the strict requirements for computational complexity, memory and power consumption. The CNNs have to be compressed and accelerated before deployment. In order to solve this problem the novel approach combining two known methods, low-rank tensor approximation in Tucker format and quantization of weights and feature maps (activations), is proposed. The greedy one-step and multi-step algorithms for the task of multilinear rank selection are proposed. The approach for quality restoration after applying Tucker decomposition and quantization is developed. The efficiency of our method is demonstrated for ResNet18 and ResNet34 on CIFAR-10, CIFAR-100 and Imagenet classification tasks. As a result of comparative analysis performed for other methods for compression and acceleration our approach showed its promising features.