Alexandr Katrutsa
Memory-Efficient Backpropagation through Large Linear Layers
Feb 02, 2022

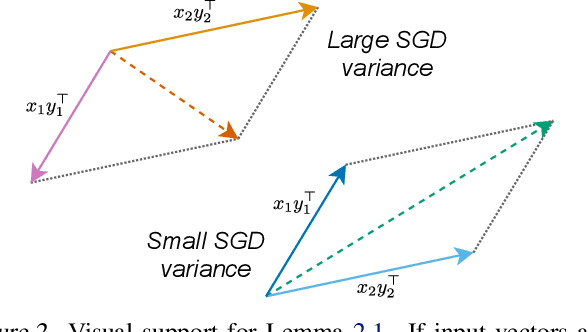

Abstract:In modern neural networks like Transformers, linear layers require significant memory to store activations during backward pass. This study proposes a memory reduction approach to perform backpropagation through linear layers. Since the gradients of linear layers are computed by matrix multiplications, we consider methods for randomized matrix multiplications and demonstrate that they require less memory with a moderate decrease of the test accuracy. Also, we investigate the variance of the gradient estimate induced by the randomized matrix multiplication. We compare this variance with the variance coming from gradient estimation based on the batch of samples. We demonstrate the benefits of the proposed method on the fine-tuning of the pre-trained RoBERTa model on GLUE tasks.
Meta-Solver for Neural Ordinary Differential Equations
Mar 15, 2021
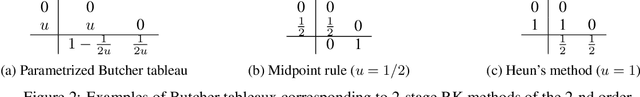

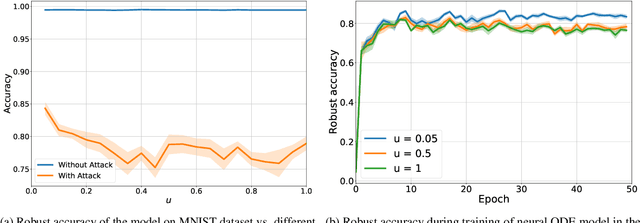
Abstract:A conventional approach to train neural ordinary differential equations (ODEs) is to fix an ODE solver and then learn the neural network's weights to optimize a target loss function. However, such an approach is tailored for a specific discretization method and its properties, which may not be optimal for the selected application and yield the overfitting to the given solver. In our paper, we investigate how the variability in solvers' space can improve neural ODEs performance. We consider a family of Runge-Kutta methods that are parameterized by no more than two scalar variables. Based on the solvers' properties, we propose an approach to decrease neural ODEs overfitting to the pre-defined solver, along with a criterion to evaluate such behaviour. Moreover, we show that the right choice of solver parameterization can significantly affect neural ODEs models in terms of robustness to adversarial attacks. Recently it was shown that neural ODEs demonstrate superiority over conventional CNNs in terms of robustness. Our work demonstrates that the model robustness can be further improved by optimizing solver choice for a given task. The source code to reproduce our experiments is available at https://github.com/juliagusak/neural-ode-metasolver.
Follow the bisector: a simple method for multi-objective optimization
Jul 14, 2020Abstract:This study presents a novel Equiangular Direction Method (EDM) to solve a multi-objective optimization problem. We consider optimization problems, where multiple differentiable losses have to be minimized. The presented method computes descent direction in every iteration to guarantee equal relative decrease of objective functions. This descent direction is based on the normalized gradients of the individual losses. Therefore, it is appropriate to solve multi-objective optimization problems with multi-scale losses. We test the proposed method on the imbalanced classification problem and multi-task learning problem, where standard datasets are used. EDM is compared with other methods to solve these problems.
Towards Understanding Normalization in Neural ODEs
Apr 27, 2020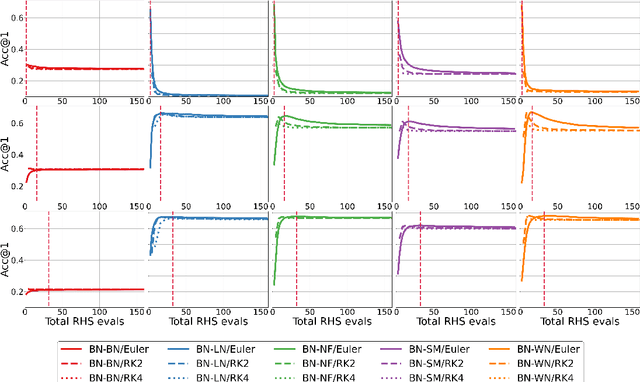
Abstract:Normalization is an important and vastly investigated technique in deep learning. However, its role for Ordinary Differential Equation based networks (neural ODEs) is still poorly understood. This paper investigates how different normalization techniques affect the performance of neural ODEs. Particularly, we show that it is possible to achieve 93% accuracy in the CIFAR-10 classification task, and to the best of our knowledge, this is the highest reported accuracy among neural ODEs tested on this problem.
Interpolated Adjoint Method for Neural ODEs
Mar 11, 2020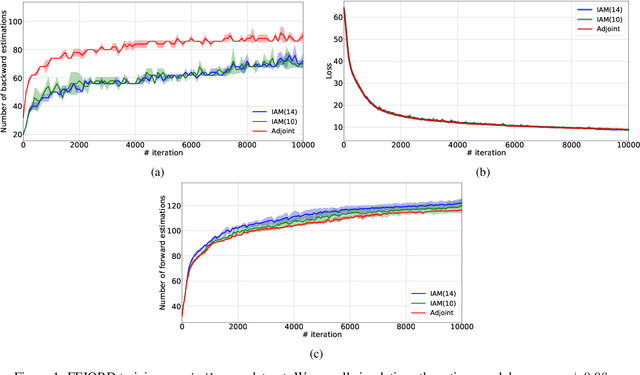
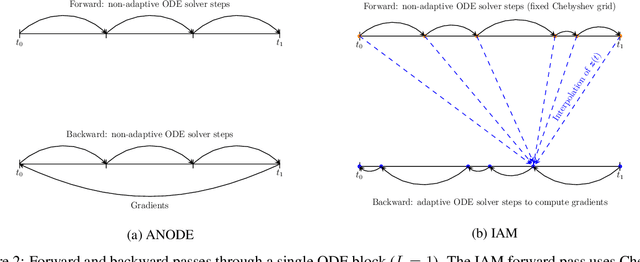

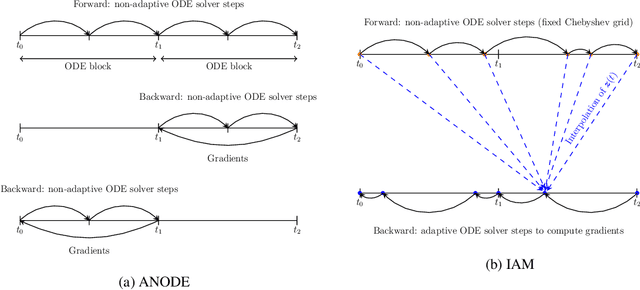
Abstract:In this paper, we propose a method, which allows us to alleviate or completely avoid the notorious problem of numerical instability and stiffness of the adjoint method for training neural ODE. On the backward pass, we propose to use the machinery of smooth function interpolation to restore the trajectory obtained during the forward integration. We show the viability of our approach, both in theory and practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge