Aleksandr Mikhalev
NNTile: a machine learning framework capable of training extremely large GPT language models on a single node
Apr 17, 2025Abstract:This study presents an NNTile framework for training large deep neural networks in heterogeneous clusters. The NNTile is based on a StarPU library, which implements task-based parallelism and schedules all provided tasks onto all available processing units (CPUs and GPUs). It means that a particular operation, necessary to train a large neural network, can be performed on any of the CPU cores or GPU devices, depending on automatic scheduling decisions. Such an approach shifts the burden of deciding where to compute and when to communicate from a human being to an automatic decision maker, whether a simple greedy heuristic or a complex AI-based software. The performance of the presented tool for training large language models is demonstrated in extensive numerical experiments.
Quantization of Large Language Models with an Overdetermined Basis
Apr 15, 2024Abstract:In this paper, we introduce an algorithm for data quantization based on the principles of Kashin representation. This approach hinges on decomposing any given vector, matrix, or tensor into two factors. The first factor maintains a small infinity norm, while the second exhibits a similarly constrained norm when multiplied by an orthogonal matrix. Surprisingly, the entries of factors after decomposition are well-concentrated around several peaks, which allows us to efficiently replace them with corresponding centroids for quantization purposes. We study the theoretical properties of the proposed approach and rigorously evaluate our compression algorithm in the context of next-word prediction tasks and on a set of downstream tasks for text classification. Our findings demonstrate that Kashin Quantization achieves competitive or superior quality in model performance while ensuring data compression, marking a significant advancement in the field of data quantization.
LoTR: Low Tensor Rank Weight Adaptation
Feb 05, 2024Abstract:In this paper we generalize and extend an idea of low-rank adaptation (LoRA) of large language models (LLMs) based on Transformer architecture. Widely used LoRA-like methods of fine-tuning LLMs are based on matrix factorization of gradient update. We introduce LoTR, a novel approach for parameter-efficient fine-tuning of LLMs which represents a gradient update to parameters in a form of tensor decomposition. Low-rank adapter for each layer is constructed as a product of three matrices, and tensor structure arises from sharing left and right multipliers of this product among layers. Simultaneous compression of a sequence of layers with low-rank tensor representation allows LoTR to archive even better parameter efficiency then LoRA especially for deep models. Moreover, the core tensor does not depend on original weight dimension and can be made arbitrary small, which allows for extremely cheap and fast downstream fine-tuning.
Run LoRA Run: Faster and Lighter LoRA Implementations
Dec 06, 2023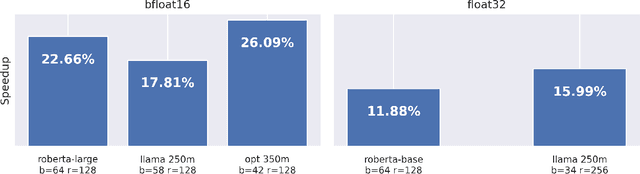

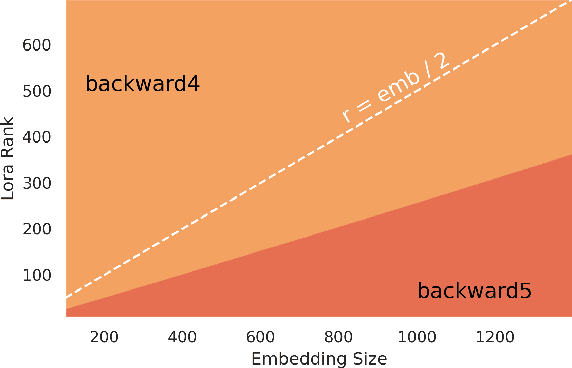
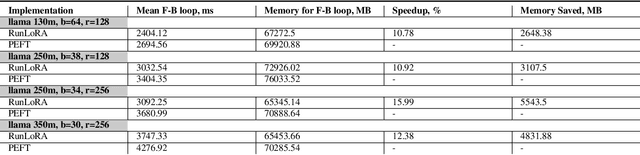
Abstract:LoRA is a technique that reduces the number of trainable parameters in a neural network by introducing low-rank adapters to linear layers. This technique is used both for fine-tuning (LoRA, QLoRA) and full train (ReLoRA). This paper presents the RunLoRA framework for efficient implementations of LoRA that significantly improves the speed of neural network training and fine-tuning using low-rank adapters. The proposed implementation optimizes the computation of LoRA operations based on dimensions of corresponding linear layer, layer input dimensions and lora rank by choosing best forward and backward computation graph based on FLOPs and time estimations, resulting in faster training without sacrificing accuracy. The experimental results show up to 17% speedup on Llama family of models.
Memory-Efficient Backpropagation through Large Linear Layers
Feb 02, 2022

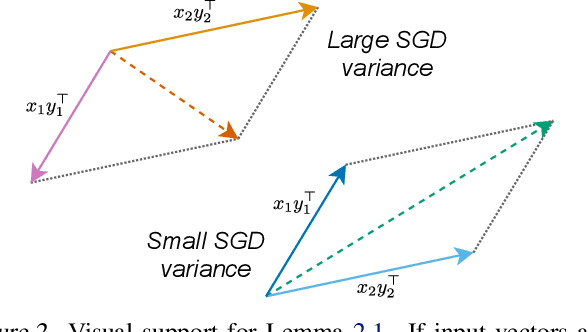

Abstract:In modern neural networks like Transformers, linear layers require significant memory to store activations during backward pass. This study proposes a memory reduction approach to perform backpropagation through linear layers. Since the gradients of linear layers are computed by matrix multiplications, we consider methods for randomized matrix multiplications and demonstrate that they require less memory with a moderate decrease of the test accuracy. Also, we investigate the variance of the gradient estimate induced by the randomized matrix multiplication. We compare this variance with the variance coming from gradient estimation based on the batch of samples. We demonstrate the benefits of the proposed method on the fine-tuning of the pre-trained RoBERTa model on GLUE tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge