Fast and Feasible: Permutation-based Constrained Reranking for Revenue Maximization

Search and recommender systems have produced highly relevant search results. A natural next step in the development of such systems in e-commerce is to rerank these results to increase the platform's revenue from paid promotion products. However, maximizing revenue alone may degrade the user experience by reducing relevance or increasing fraud risk. To avoid this, we state the reranking problem as an integer linear program ($ILP$) that maximizes revenue subject to per-query constraints on other metrics, e.g., relevance. Since solving $ILP$ exactly for every query is slow for deployment to the online service, we propose a lightweight permutation-based reranking approximation algorithm PermR. At each step, the algorithm selects a pair of neighboring items and swaps them to either improve the objective or repair a violated constraint. We evaluate PermR across multiple categories of a large classified platform in offline and online settings. PermR achieves about 63\% of the ILP revenue improvement, within production latency limits, preserving all constraints. In a 14-day online A/B test over 56 million search queries, PermR increased revenue by $2$\%.

Uncertainty Quantification of Click and Conversion Estimates for the Autobidding

Modern e-commerce platforms employ various auction mechanisms to allocate paid slots for a given item. To scale this approach to the millions of auctions, the platforms suggest promotion tools based on the autobidding algorithms. These algorithms typically depend on the Click-Through-Rate (CTR) and Conversion-Rate (CVR) estimates provided by a pre-trained machine learning model. However, the predictions of such models are uncertain and can significantly affect the performance of the autobidding algorithm. To address this issue, we propose the DenoiseBid method, which corrects the generated CTRs and CVRs to make the resulting bids more efficient in auctions. The underlying idea of our method is to employ a Bayesian approach and replace noisy CTR or CVR estimates with those from recovered distributions. To demonstrate the performance of the proposed approach, we perform extensive experiments on the synthetic, iPinYou, and BAT datasets. To evaluate the robustness of our approach to the noise scale, we use synthetic noise and noise estimated from the predictions of the pre-trained machine learning model.

Empirical evaluation of the Frank-Wolfe methods for constructing white-box adversarial attacks

The construction of adversarial attacks for neural networks appears to be a crucial challenge for their deployment in various services. To estimate the adversarial robustness of a neural network, a fast and efficient approach is needed to construct adversarial attacks. Since the formalization of adversarial attack construction involves solving a specific optimization problem, we consider the problem of constructing an efficient and effective adversarial attack from a numerical optimization perspective. Specifically, we suggest utilizing advanced projection-free methods, known as modified Frank-Wolfe methods, to construct white-box adversarial attacks on the given input data. We perform a theoretical and numerical evaluation of these methods and compare them with standard approaches based on projection operations or geometrical intuition. Numerical experiments are performed on the MNIST and CIFAR-10 datasets, utilizing a multiclass logistic regression model, the convolutional neural networks (CNNs), and the Vision Transformer (ViT).

Dynamic Low-rank Approximation of Full-Matrix Preconditioner for Training Generalized Linear Models

Adaptive gradient methods like Adagrad and its variants are widespread in large-scale optimization. However, their use of diagonal preconditioning matrices limits the ability to capture parameter correlations. Full-matrix adaptive methods, approximating the exact Hessian, can model these correlations and may enable faster convergence. At the same time, their computational and memory costs are often prohibitive for large-scale models. To address this limitation, we propose AdaGram, an optimizer that enables efficient full-matrix adaptive gradient updates. To reduce memory and computational overhead, we utilize fast symmetric factorization for computing the preconditioned update direction at each iteration. Additionally, we maintain the low-rank structure of a preconditioner along the optimization trajectory using matrix integrator methods. Numerical experiments on standard machine learning tasks show that AdaGram converges faster or matches the performance of diagonal adaptive optimizers when using rank five and smaller rank approximations. This demonstrates AdaGram's potential as a scalable solution for adaptive optimization in large models.

NNTile: a machine learning framework capable of training extremely large GPT language models on a single node

This study presents an NNTile framework for training large deep neural networks in heterogeneous clusters. The NNTile is based on a StarPU library, which implements task-based parallelism and schedules all provided tasks onto all available processing units (CPUs and GPUs). It means that a particular operation, necessary to train a large neural network, can be performed on any of the CPU cores or GPU devices, depending on automatic scheduling decisions. Such an approach shifts the burden of deciding where to compute and when to communicate from a human being to an automatic decision maker, whether a simple greedy heuristic or a complex AI-based software. The performance of the presented tool for training large language models is demonstrated in extensive numerical experiments.

Fast UCB-type algorithms for stochastic bandits with heavy and super heavy symmetric noise

In this study, we propose a new method for constructing UCB-type algorithms for stochastic multi-armed bandits based on general convex optimization methods with an inexact oracle. We derive the regret bounds corresponding to the convergence rates of the optimization methods. We propose a new algorithm Clipped-SGD-UCB and show, both theoretically and empirically, that in the case of symmetric noise in the reward, we can achieve an $O(\log T\sqrt{KT\log T})$ regret bound instead of $O\left (T^{\frac{1}{1+\alpha}} K^{\frac{\alpha}{1+\alpha}} \right)$ for the case when the reward distribution satisfies $\mathbb{E}_{X \in D}[|X|^{1+\alpha}] \leq \sigma^{1+\alpha}$ ($\alpha \in (0, 1])$, i.e. perform better than it is assumed by the general lower bound for bandits with heavy-tails. Moreover, the same bound holds even when the reward distribution does not have the expectation, that is, when $\alpha<0$.

Memory-efficient particle filter recurrent neural network for object localization

This study proposes a novel memory-efficient recurrent neural network (RNN) architecture specified to solve the object localization problem. This problem is to recover the object states along with its movement in a noisy environment. We take the idea of the classical particle filter and combine it with GRU RNN architecture. The key feature of the resulting memory-efficient particle filter RNN model (mePFRNN) is that it requires the same number of parameters to process environments of different sizes. Thus, the proposed mePFRNN architecture consumes less memory to store parameters compared to the previously proposed PFRNN model. To demonstrate the performance of our model, we test it on symmetric and noisy environments that are incredibly challenging for filtering algorithms. In our experiments, the mePFRNN model provides more precise localization than the considered competitors and requires fewer trained parameters.

Multiparticle Kalman filter for object localization in symmetric environments

This study considers the object localization problem and proposes a novel multiparticle Kalman filter to solve it in complex and symmetric environments. Two well-known classes of filtering algorithms to solve the localization problem are Kalman filter-based methods and particle filter-based methods. We consider these classes, demonstrate their complementary properties, and propose a novel filtering algorithm that takes the best from two classes. We evaluate the multiparticle Kalman filter in symmetric and noisy environments. Such environments are especially challenging for both classes of classical methods. We compare the proposed approach with the particle filter since only this method is feasible if the initial state is unknown. In the considered challenging environments, our method outperforms the particle filter in terms of both localization error and runtime.

NAG-GS: Semi-Implicit, Accelerated and Robust Stochastic Optimizers

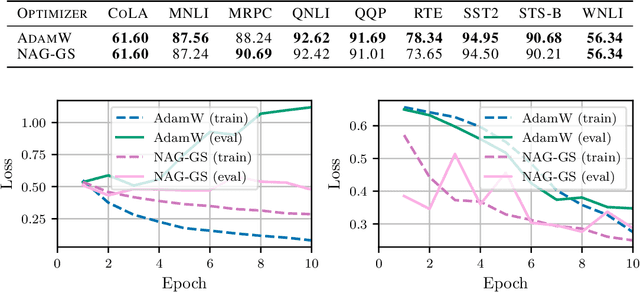
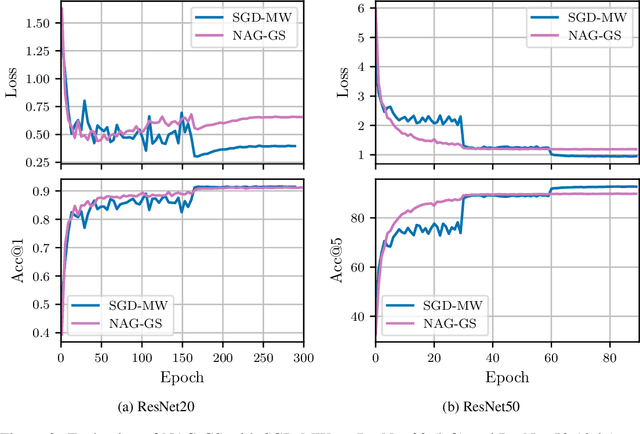
Classical machine learning models such as deep neural networks are usually trained by using Stochastic Gradient Descent-based (SGD) algorithms. The classical SGD can be interpreted as a discretization of the stochastic gradient flow. In this paper we propose a novel, robust and accelerated stochastic optimizer that relies on two key elements: (1) an accelerated Nesterov-like Stochastic Differential Equation (SDE) and (2) its semi-implicit Gauss-Seidel type discretization. The convergence and stability of the obtained method, referred to as NAG-GS, are first studied extensively in the case of the minimization of a quadratic function. This analysis allows us to come up with an optimal step size (or learning rate) in terms of rate of convergence while ensuring the stability of NAG-GS. This is achieved by the careful analysis of the spectral radius of the iteration matrix and the covariance matrix at stationarity with respect to all hyperparameters of our method. We show that NAG-GS is competitive with state-of-the-art methods such as momentum SGD with weight decay and AdamW for the training of machine learning models such as the logistic regression model, the residual networks models on standard computer vision datasets, and Transformers in the frame of the GLUE benchmark.

Extension of Dynamic Mode Decomposition for dynamic systems with incomplete information based on t-model of optimal prediction

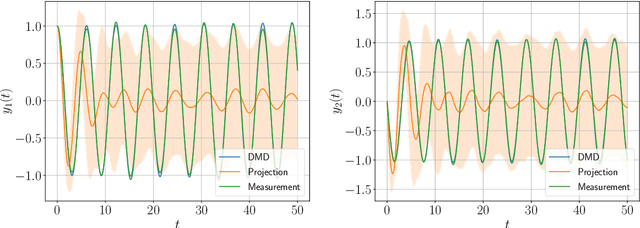
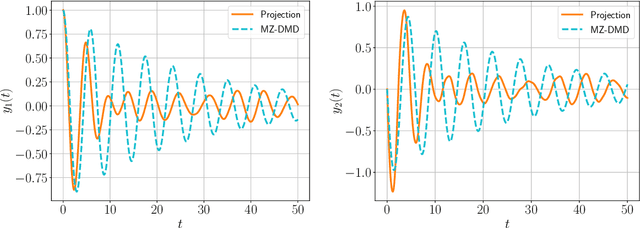
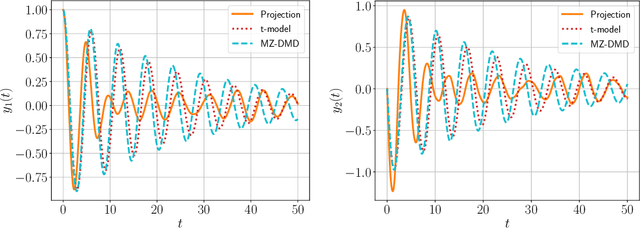
The Dynamic Mode Decomposition has proved to be a very efficient technique to study dynamic data. This is entirely a data-driven approach that extracts all necessary information from data snapshots which are commonly supposed to be sampled from measurement. The application of this approach becomes problematic if the available data is incomplete because some dimensions of smaller scale either missing or unmeasured. Such setting occurs very often in modeling complex dynamical systems such as power grids, in particular with reduced-order modeling. To take into account the effect of unresolved variables the optimal prediction approach based on the Mori-Zwanzig formalism can be applied to obtain the most expected prediction under existing uncertainties. This effectively leads to the development of a time-predictive model accounting for the impact of missing data. In the present paper we provide a detailed derivation of the considered method from the Liouville equation and finalize it with the optimization problem that defines the optimal transition operator corresponding to the observed data. In contrast to the existing approach, we consider a first-order approximation of the Mori-Zwanzig decomposition, state the corresponding optimization problem and solve it with the gradient-based optimization method. The gradient of the obtained objective function is computed precisely through the automatic differentiation technique. The numerical experiments illustrate that the considered approach gives practically the same dynamics as the exact Mori-Zwanzig decomposition, but is less computationally intensive.