Safe Risk-averse Bayesian Optimization for Controller Tuning

Controller tuning and parameter optimization are crucial in system design to improve both the controller and underlying system performance. Bayesian optimization has been established as an efficient model-free method for controller tuning and adaptation. Standard methods, however, are not enough for high-precision systems to be robust with respect to unknown input-dependent noise and stable under safety constraints. In this work, we present a novel data-driven approach, RaGoOSE, for safe controller tuning in the presence of heteroscedastic noise, combining safe learning with risk-averse Bayesian optimization. We demonstrate the method for synthetic benchmark and compare its performance to established BO-based tuning methods. We further evaluate RaGoOSE performance on a real precision-motion system utilized in semiconductor industry applications and compare it to the built-in auto-tuning routine.

Cherry-Picking Gradients: Learning Low-Rank Embeddings of Visual Data via Differentiable Cross-Approximation

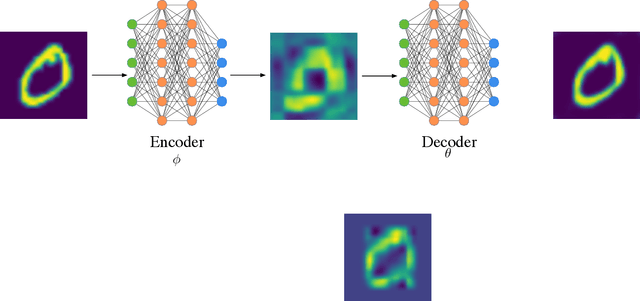
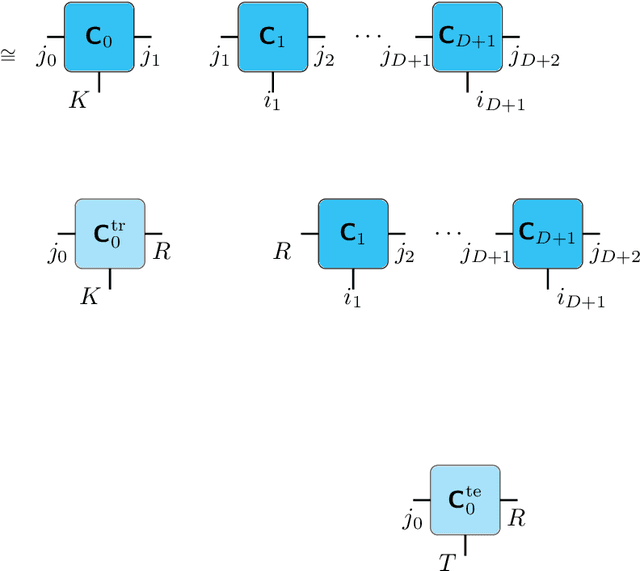
We propose an end-to-end trainable framework that processes large-scale visual data tensors by looking \emph{at a fraction of their entries only}. Our method combines a neural network encoder with a \emph{tensor train decomposition} to learn a low-rank latent encoding, coupled with cross-approximation (CA) to learn the representation through a subset of the original samples. CA is an adaptive sampling algorithm that is native to tensor decompositions and avoids working with the full high-resolution data explicitly. Instead, it actively selects local representative samples that we fetch out-of-core and on-demand. The required number of samples grows only logarithmically with the size of the input. Our implicit representation of the tensor in the network enables processing large grids that could not be otherwise tractable in their uncompressed form. The proposed approach is particularly useful for large-scale multidimensional grid data (e.g., 3D tomography), and for tasks that require context over a large receptive field (e.g., predicting the medical condition of entire organs). The code will be available at https://github.com/aelphy/c-pic

Overfitting in Bayesian Optimization: an empirical study and early-stopping solution

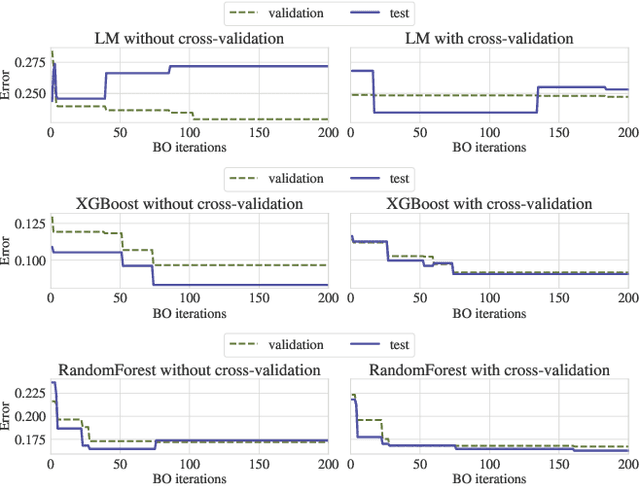
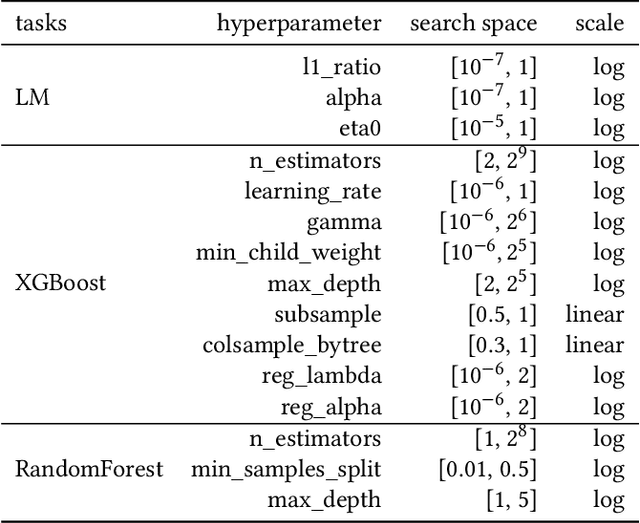
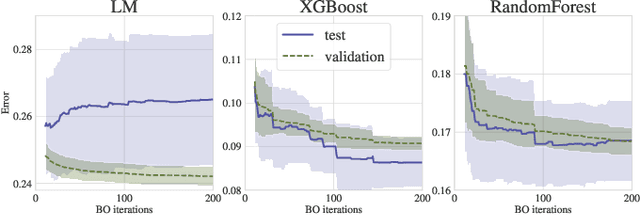
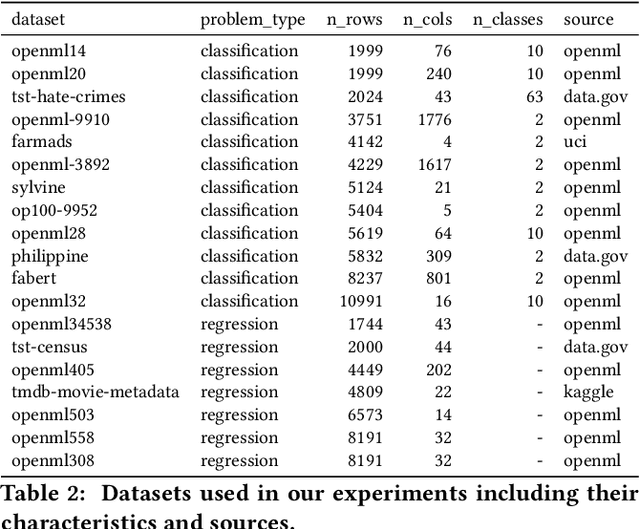
Bayesian Optimization (BO) is a successful methodology to tune the hyperparameters of machine learning algorithms. The user defines a metric of interest, such as the validation error, and BO finds the optimal hyperparameters that minimize it. However, the metric improvements on the validation set may not translate to the test set, especially on small datasets. In other words, BO can overfit. While cross-validation mitigates this, it comes with high computational cost. In this paper, we carry out the first systematic investigation of overfitting in BO and demonstrate that this is a serious yet often overlooked concern in practice. We propose the first problem-adaptive and interpretable criterion to early stop BO, reducing overfitting while mitigating the cost of cross-validation. Experimental results on real-world hyperparameter optimization tasks show that our approach can substantially reduce compute time with little to no loss of test accuracy,demonstrating a clear practical advantage over existing techniques.

Hierarchical Image Classification using Entailment Cone Embeddings

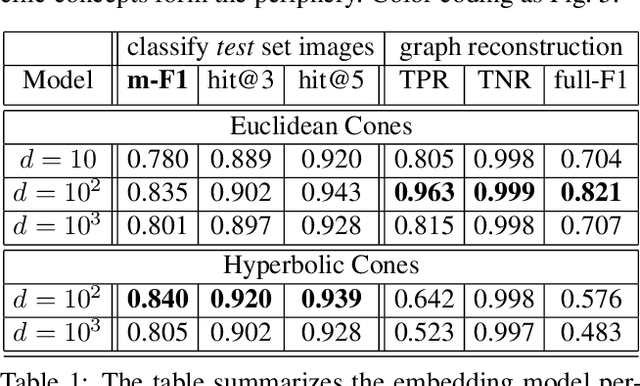
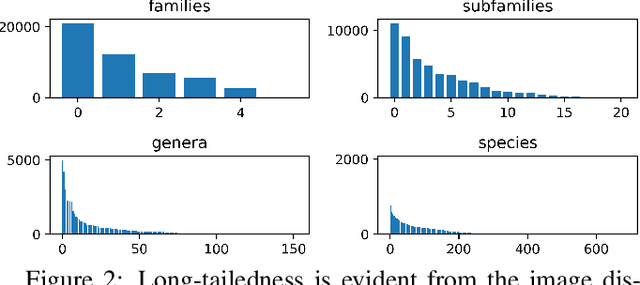
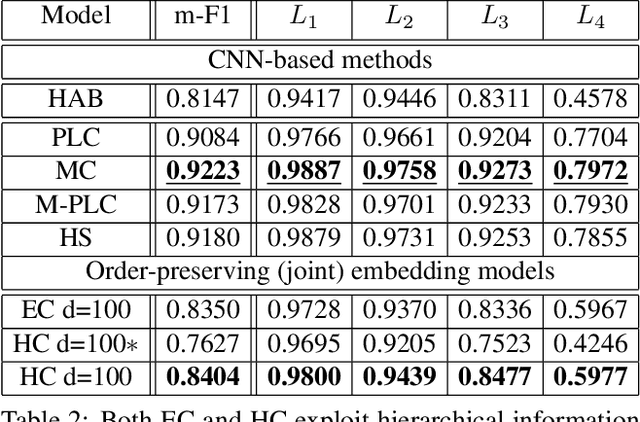
Image classification has been studied extensively, but there has been limited work in using unconventional, external guidance other than traditional image-label pairs for training. We present a set of methods for leveraging information about the semantic hierarchy embedded in class labels. We first inject label-hierarchy knowledge into an arbitrary CNN-based classifier and empirically show that availability of such external semantic information in conjunction with the visual semantics from images boosts overall performance. Taking a step further in this direction, we model more explicitly the label-label and label-image interactions using order-preserving embeddings governed by both Euclidean and hyperbolic geometries, prevalent in natural language, and tailor them to hierarchical image classification and representation learning. We empirically validate all the models on the hierarchical ETHEC dataset.

Mixed-Variable Bayesian Optimization

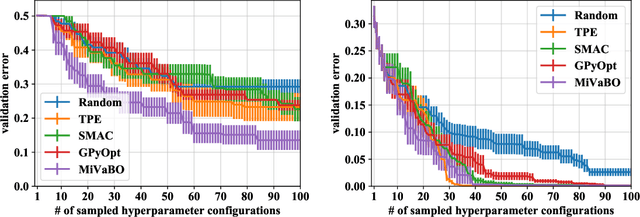
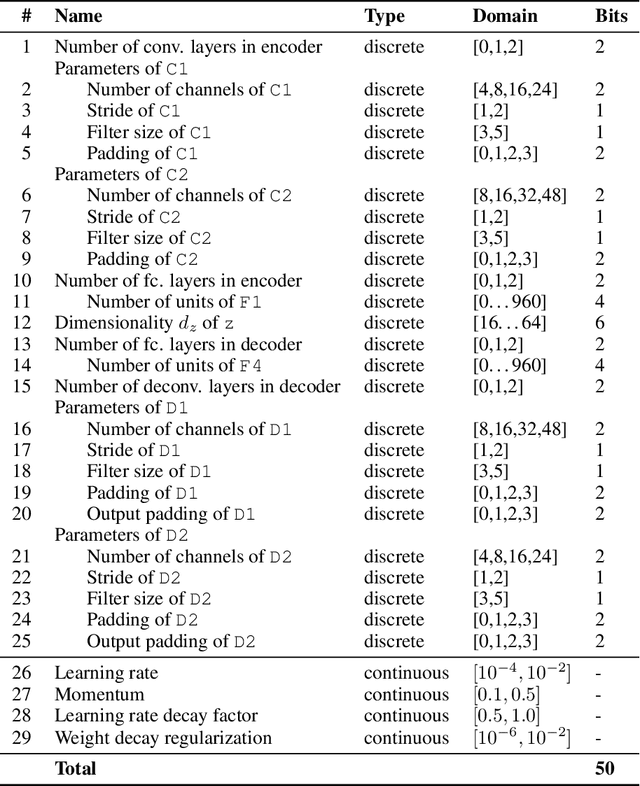
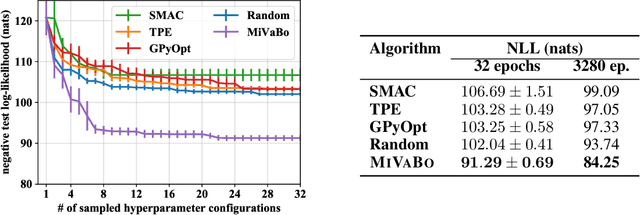
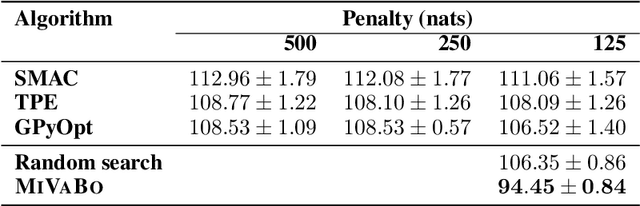
The optimization of expensive to evaluate, black-box, mixed-variable functions, i.e. functions that have continuous and discrete inputs, is a difficult and yet pervasive problem in science and engineering. In Bayesian optimization (BO), special cases of this problem that consider fully continuous or fully discrete domains have been widely studied. However, few methods exist for mixed-variable domains. In this paper, we introduce MiVaBo, a novel BO algorithm for the efficient optimization of mixed-variable functions that combines a linear surrogate model based on expressive feature representations with Thompson sampling. We propose two methods to optimize its acquisition function, a challenging problem for mixed-variable domains, and we show that MiVaBo can handle complex constraints over the discrete part of the domain that other methods cannot take into account. Moreover, we provide the first convergence analysis of a mixed-variable BO algorithm. Finally, we show that MiVaBo is significantly more sample efficient than state-of-the-art mixed-variable BO algorithms on hyperparameter tuning tasks.