Classifying the evolution of COVID-19 severity on patients with combined dynamic Bayesian networks and neural networks

When we face patients arriving to a hospital suffering from the effects of some illness, one of the main problems we can encounter is evaluating whether or not said patients are going to require intensive care in the near future. This intensive care requires allotting valuable and scarce resources, and knowing beforehand the severity of a patients illness can improve both its treatment and the organization of resources. We illustrate this issue in a dataset consistent of Spanish COVID-19 patients from the sixth epidemic wave where we label patients as critical when they either had to enter the intensive care unit or passed away. We then combine the use of dynamic Bayesian networks, to forecast the vital signs and the blood analysis results of patients over the next 40 hours, and neural networks, to evaluate the severity of a patients disease in that interval of time. Our empirical results show that the transposition of the current state of a patient to future values with the DBN for its subsequent use in classification obtains better the accuracy and g-mean score than a direct application with a classifier.

Context-specific kernel-based hidden Markov model for time series analysis

Traditional hidden Markov models have been a useful tool to understand and model stochastic dynamic linear data; in the case of non-Gaussian data or not linear in mean data, models such as mixture of Gaussian hidden Markov models suffer from the computation of precision matrices and have a lot of unnecessary parameters. As a consequence, such models often perform better when it is assumed that all variables are independent, a hypothesis that may be unrealistic. Hidden Markov models based on kernel density estimation is also capable of modeling non Gaussian data, but they assume independence between variables. In this article, we introduce a new hidden Markov model based on kernel density estimation, which is capable of introducing kernel dependencies using context-specific Bayesian networks. The proposed model is described, together with a learning algorithm based on the expectation-maximization algorithm. Additionally, the model is compared with related HMMs using synthetic and real data. From the results, the benefits in likelihood and classification accuracy from the proposed model are quantified and analyzed.

Quantum Approximate Optimization Algorithm for Bayesian network structure learning

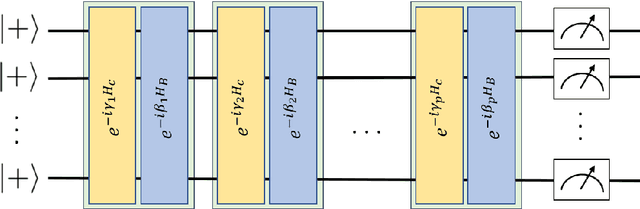
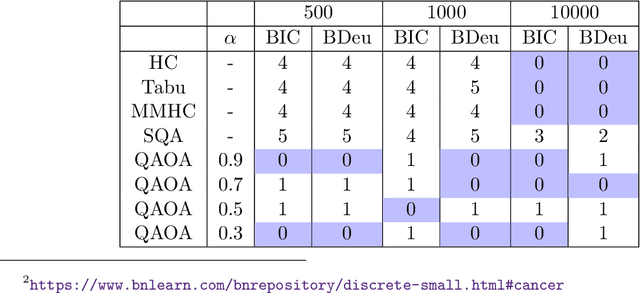
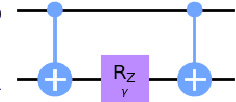
Bayesian network structure learning is an NP-hard problem that has been faced by a number of traditional approaches in recent decades. Currently, quantum technologies offer a wide range of advantages that can be exploited to solve optimization tasks that cannot be addressed in an efficient way when utilizing classic computing approaches. In this work, a specific type of variational quantum algorithm, the quantum approximate optimization algorithm, was used to solve the Bayesian network structure learning problem, by employing $3n(n-1)/2$ qubits, where $n$ is the number of nodes in the Bayesian network to be learned. Our results showed that the quantum approximate optimization algorithm approach offers competitive results with state-of-the-art methods and quantitative resilience to quantum noise. The approach was applied to a cancer benchmark problem, and the results justified the use of variational quantum algorithms for solving the Bayesian network structure learning problem.

Semiparametric Bayesian Networks

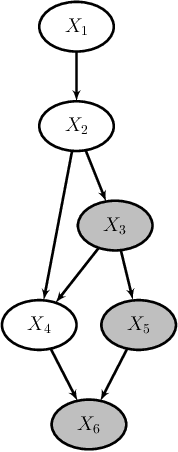
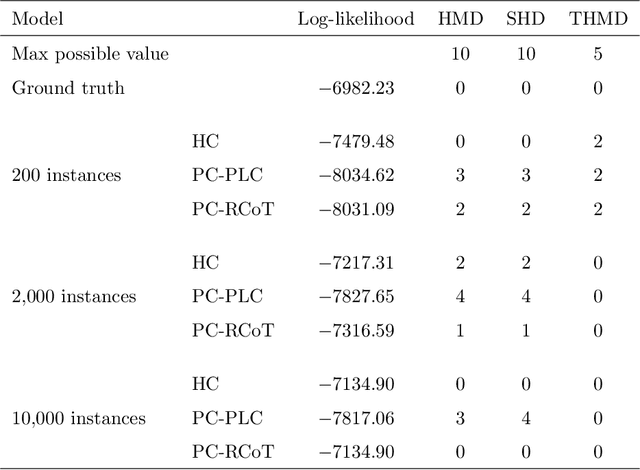
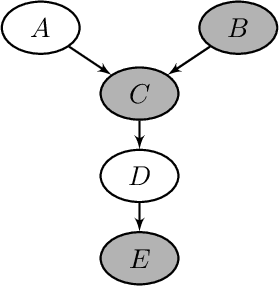
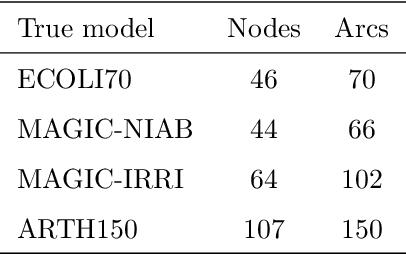
We introduce semiparametric Bayesian networks that combine parametric and nonparametric conditional probability distributions. Their aim is to incorporate the advantages of both components: the bounded complexity of parametric models and the flexibility of nonparametric ones. We demonstrate that semiparametric Bayesian networks generalize two well-known types of Bayesian networks: Gaussian Bayesian networks and kernel density estimation Bayesian networks. For this purpose, we consider two different conditional probability distributions required in a semiparametric Bayesian network. In addition, we present modifications of two well-known algorithms (greedy hill-climbing and PC) to learn the structure of a semiparametric Bayesian network from data. To realize this, we employ a score function based on cross-validation. In addition, using a validation dataset, we apply an early-stopping criterion to avoid overfitting. To evaluate the applicability of the proposed algorithm, we conduct an exhaustive experiment on synthetic data sampled by mixing linear and nonlinear functions, multivariate normal data sampled from Gaussian Bayesian networks, real data from the UCI repository, and bearings degradation data. As a result of this experiment, we conclude that the proposed algorithm accurately learns the combination of parametric and nonparametric components, while achieving a performance comparable with those provided by state-of-the-art methods.

Autoregressive Asymmetric Linear Gaussian Hidden Markov Models

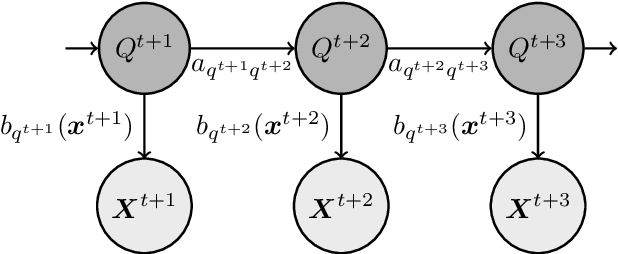
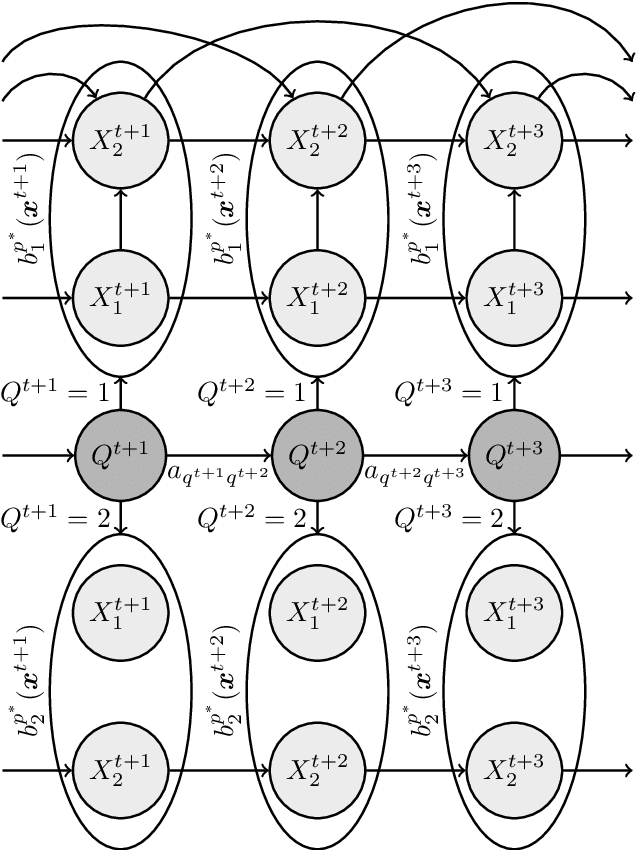
In a real life process evolving over time, the relationship between its relevant variables may change. Therefore, it is advantageous to have different inference models for each state of the process. Asymmetric hidden Markov models fulfil this dynamical requirement and provide a framework where the trend of the process can be expressed as a latent variable. In this paper, we modify these recent asymmetric hidden Markov models to have an asymmetric autoregressive component, allowing the model to choose the order of autoregression that maximizes its penalized likelihood for a given training set. Additionally, we show how inference, hidden states decoding and parameter learning must be adapted to fit the proposed model. Finally, we run experiments with synthetic and real data to show the capabilities of this new model.

Sparse Cholesky covariance parametrization for recovering latent structure in ordered data

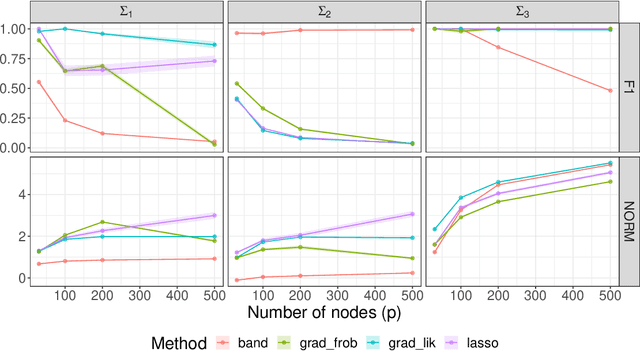
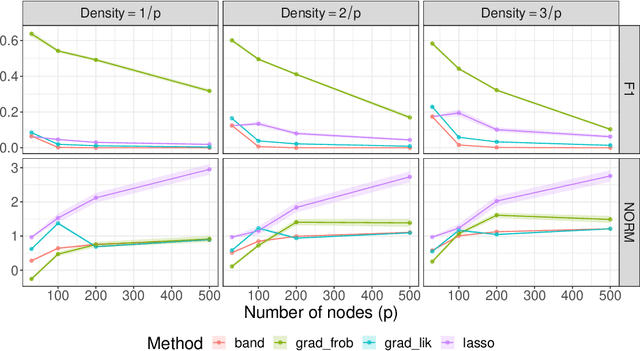
The sparse Cholesky parametrization of the inverse covariance matrix can be interpreted as a Gaussian Bayesian network; however its counterpart, the covariance Cholesky factor, has received, with few notable exceptions, little attention so far, despite having a natural interpretation as a hidden variable model for ordered signal data. To fill this gap, in this paper we focus on arbitrary zero patterns in the Cholesky factor of a covariance matrix. We discuss how these models can also be extended, in analogy with Gaussian Bayesian networks, to data where no apparent order is available. For the ordered scenario, we propose a novel estimation method that is based on matrix loss penalization, as opposed to the existing regression-based approaches. The performance of this sparse model for the Cholesky factor, together with our novel estimator, is assessed in a simulation setting, as well as over spatial and temporal real data where a natural ordering arises among the variables. We give guidelines, based on the empirical results, about which of the methods analysed is more appropriate for each setting.

Towards Gaussian Bayesian Network Fusion

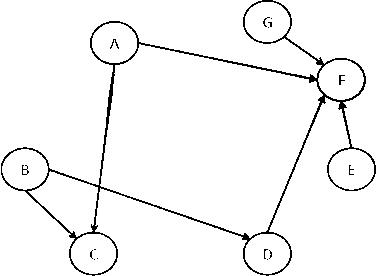
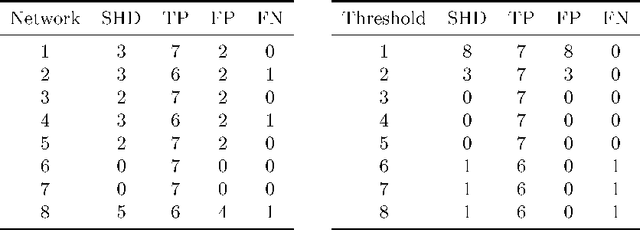
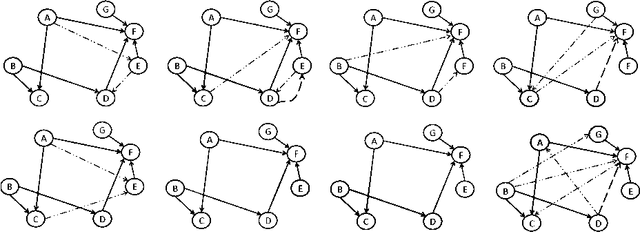
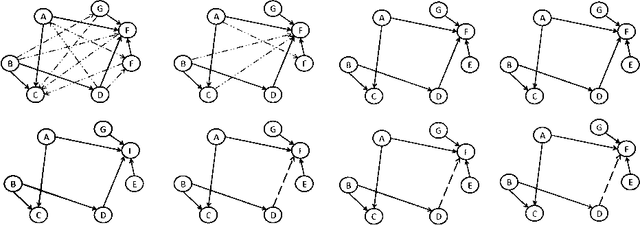
Data sets are growing in complexity thanks to the increasing facilities we have nowadays to both generate and store data. This poses many challenges to machine learning that are leading to the proposal of new methods and paradigms, in order to be able to deal with what is nowadays referred to as Big Data. In this paper we propose a method for the aggregation of different Bayesian network structures that have been learned from separate data sets, as a first step towards mining data sets that need to be partitioned in an horizontal way, i.e. with respect to the instances, in order to be processed. Considerations that should be taken into account when dealing with this situation are discussed. Scalable learning of Bayesian networks is slowly emerging, and our method constitutes one of the first insights into Gaussian Bayesian network aggregation from different sources. Tested on synthetic data it obtains good results that surpass those from individual learning. Future research will be focused on expanding the method and testing more diverse data sets.

Markov Property in Generative Classifiers

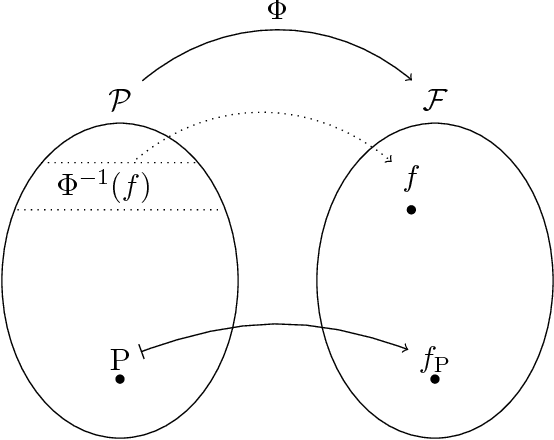
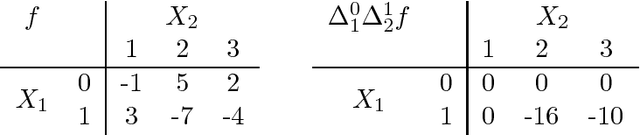
We show that, for generative classifiers, conditional independence corresponds to linear constraints for the induced discrimination functions. Discrimination functions of undirected Markov network classifiers can thus be characterized by sets of linear constraints. These constraints are represented by a second order finite difference operator over functions of categorical variables. As an application we study the expressive power of generative classifiers under the undirected Markov property and we present a general method to combine discriminative and generative classifiers.

Bayesian optimization of the PC algorithm for learning Gaussian Bayesian networks

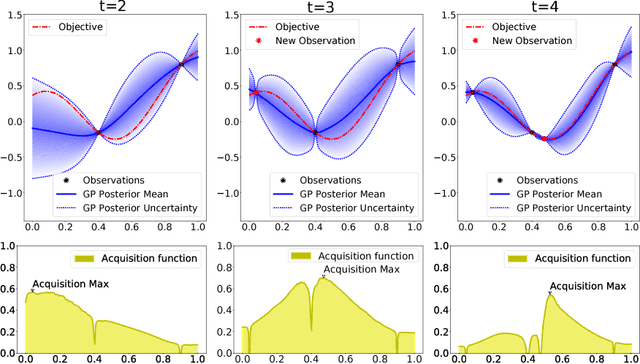
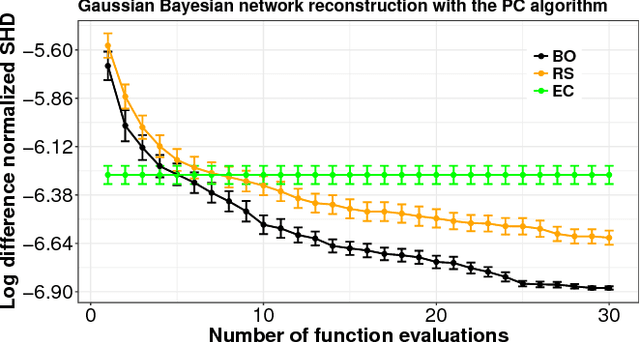
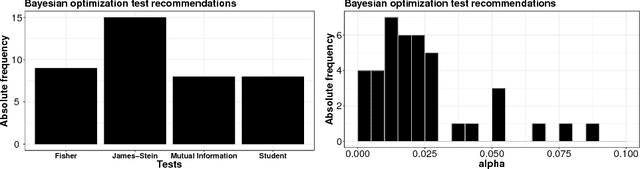
The PC algorithm is a popular method for learning the structure of Gaussian Bayesian networks. It carries out statistical tests to determine absent edges in the network. It is hence governed by two parameters: (i) The type of test, and (ii) its significance level. These parameters are usually set to values recommended by an expert. Nevertheless, such an approach can suffer from human bias, leading to suboptimal reconstruction results. In this paper we consider a more principled approach for choosing these parameters in an automatic way. For this we optimize a reconstruction score evaluated on a set of different Gaussian Bayesian networks. This objective is expensive to evaluate and lacks a closed-form expression, which means that Bayesian optimization (BO) is a natural choice. BO methods use a model to guide the search and are hence able to exploit smoothness properties of the objective surface. We show that the parameters found by a BO method outperform those found by a random search strategy and the expert recommendation. Importantly, we have found that an often overlooked statistical test provides the best over-all reconstruction results.

On Gaussian Markov models for conditional independence

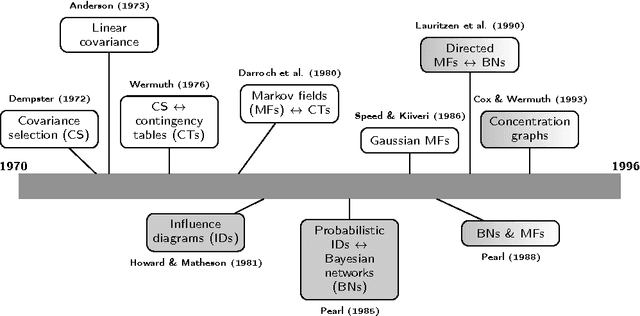
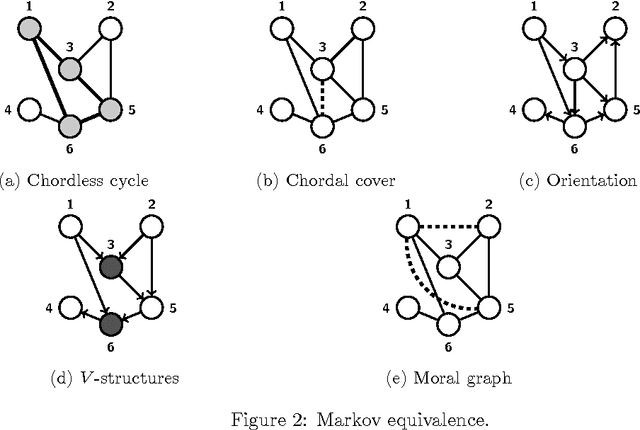
Markov models lie at the interface between statistical independence in a probability distribution and graph separation properties. We review model selection and estimation in directed and undirected Markov models with Gaussian parametrization, emphasizing the main similarities and differences. These two models are similar but not equivalent, although they share a common intersection. We present the existing results from a historical perspective, taking into account the amount of literature existing from both the artificial intelligence and statistics research communities, where these models were originated. We also discuss how the Gaussian assumption can be relaxed. We finally point out the main areas of application where these Markov models are nowadays used.