Autoregressive Asymmetric Linear Gaussian Hidden Markov Models
Paper and Code
Oct 27, 2020
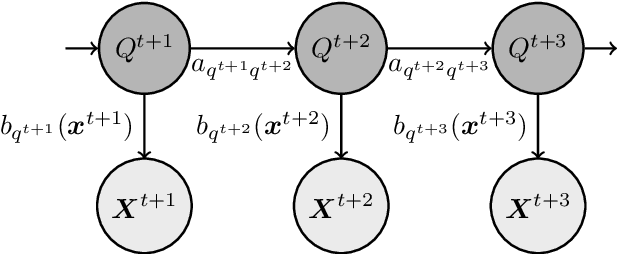

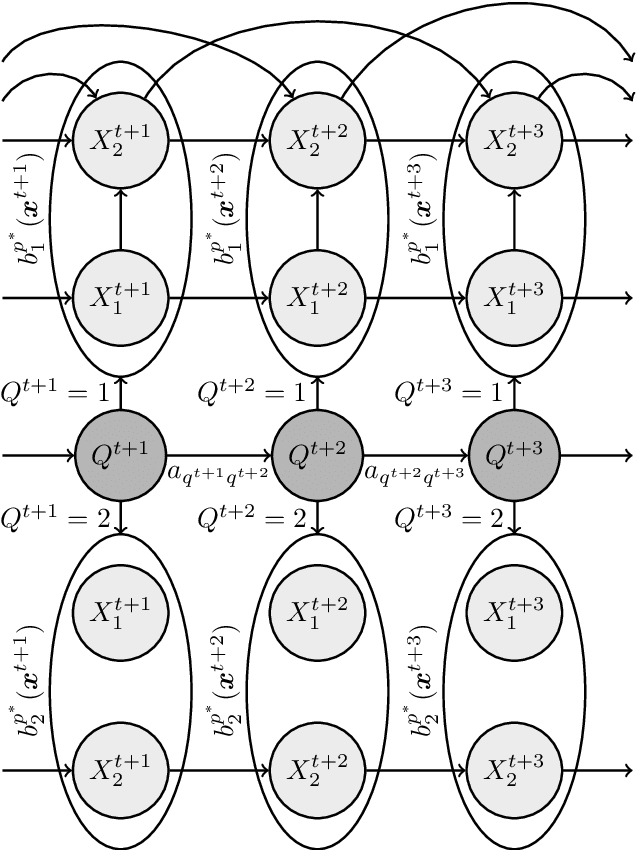
In a real life process evolving over time, the relationship between its relevant variables may change. Therefore, it is advantageous to have different inference models for each state of the process. Asymmetric hidden Markov models fulfil this dynamical requirement and provide a framework where the trend of the process can be expressed as a latent variable. In this paper, we modify these recent asymmetric hidden Markov models to have an asymmetric autoregressive component, allowing the model to choose the order of autoregression that maximizes its penalized likelihood for a given training set. Additionally, we show how inference, hidden states decoding and parameter learning must be adapted to fit the proposed model. Finally, we run experiments with synthetic and real data to show the capabilities of this new model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge