Context-specific kernel-based hidden Markov model for time series analysis

Traditional hidden Markov models have been a useful tool to understand and model stochastic dynamic linear data; in the case of non-Gaussian data or not linear in mean data, models such as mixture of Gaussian hidden Markov models suffer from the computation of precision matrices and have a lot of unnecessary parameters. As a consequence, such models often perform better when it is assumed that all variables are independent, a hypothesis that may be unrealistic. Hidden Markov models based on kernel density estimation is also capable of modeling non Gaussian data, but they assume independence between variables. In this article, we introduce a new hidden Markov model based on kernel density estimation, which is capable of introducing kernel dependencies using context-specific Bayesian networks. The proposed model is described, together with a learning algorithm based on the expectation-maximization algorithm. Additionally, the model is compared with related HMMs using synthetic and real data. From the results, the benefits in likelihood and classification accuracy from the proposed model are quantified and analyzed.

Autoregressive Asymmetric Linear Gaussian Hidden Markov Models

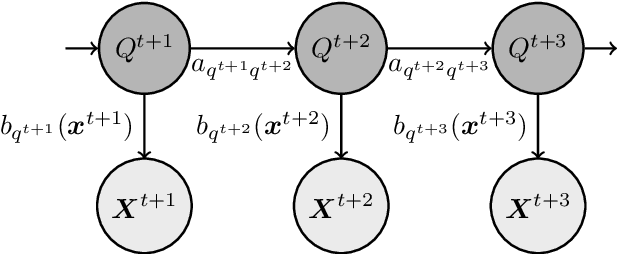
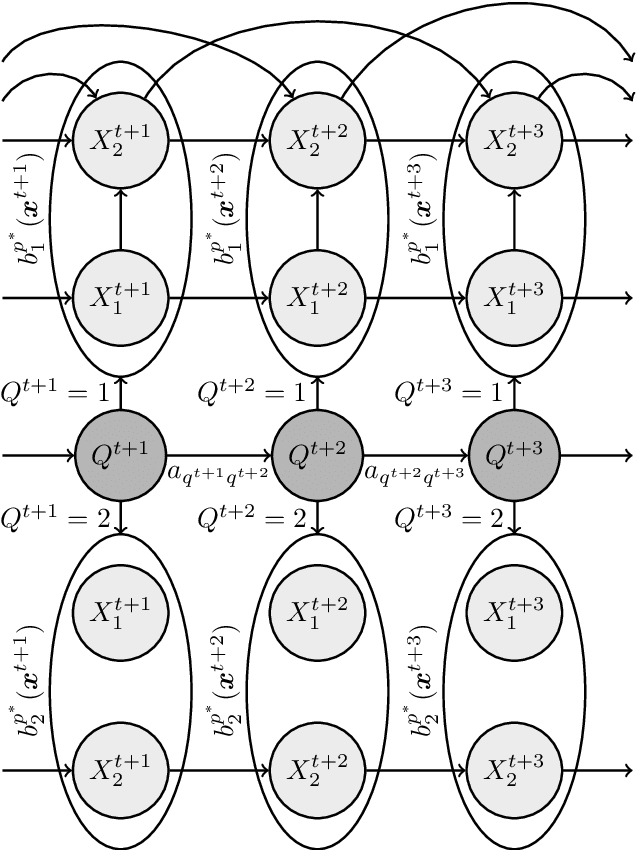
In a real life process evolving over time, the relationship between its relevant variables may change. Therefore, it is advantageous to have different inference models for each state of the process. Asymmetric hidden Markov models fulfil this dynamical requirement and provide a framework where the trend of the process can be expressed as a latent variable. In this paper, we modify these recent asymmetric hidden Markov models to have an asymmetric autoregressive component, allowing the model to choose the order of autoregression that maximizes its penalized likelihood for a given training set. Additionally, we show how inference, hidden states decoding and parameter learning must be adapted to fit the proposed model. Finally, we run experiments with synthetic and real data to show the capabilities of this new model.