Quantum Approximate Optimization Algorithm for Bayesian network structure learning
Paper and Code
Mar 04, 2022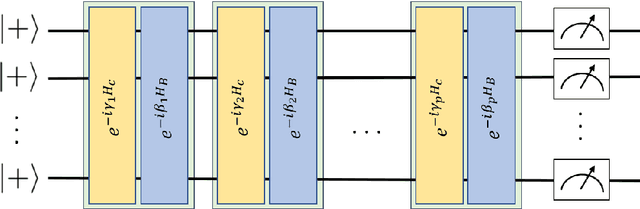
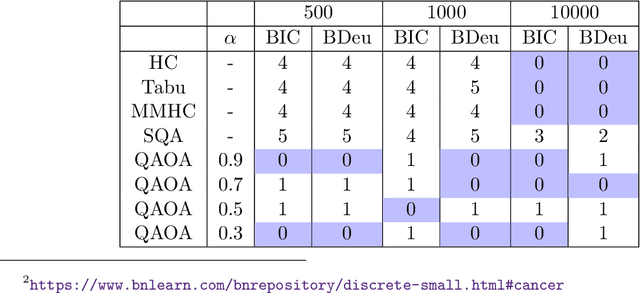
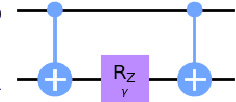
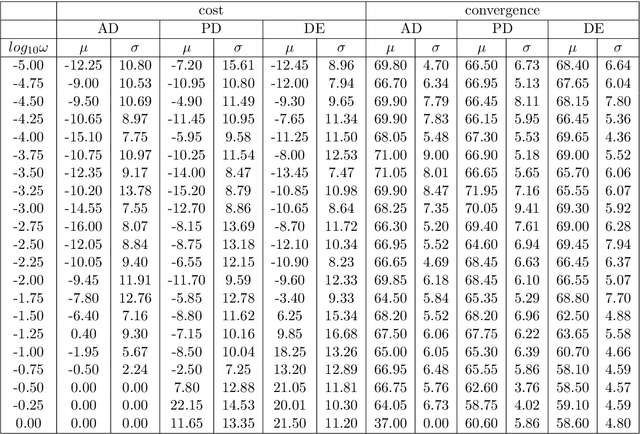
Bayesian network structure learning is an NP-hard problem that has been faced by a number of traditional approaches in recent decades. Currently, quantum technologies offer a wide range of advantages that can be exploited to solve optimization tasks that cannot be addressed in an efficient way when utilizing classic computing approaches. In this work, a specific type of variational quantum algorithm, the quantum approximate optimization algorithm, was used to solve the Bayesian network structure learning problem, by employing $3n(n-1)/2$ qubits, where $n$ is the number of nodes in the Bayesian network to be learned. Our results showed that the quantum approximate optimization algorithm approach offers competitive results with state-of-the-art methods and quantitative resilience to quantum noise. The approach was applied to a cancer benchmark problem, and the results justified the use of variational quantum algorithms for solving the Bayesian network structure learning problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge